نقشه راه GIS

درخواست مشاوره

09120049370

8 صبح تا 12 شب

09120049370

Telegram Whatsapp Youtube
کاربرد جی ای اس

 

چکیده

تحقیقات زیادی در مورد مشکلات مسیریابی در زمینه شبکه های حمل و نقل انجام شده است، در حالی که مسیریابی در فضای خارج از شبکه مورد توجه بسیار کمتری قرار گرفته است. در سیستم‌های اطلاعات جغرافیایی (GIS)، روش دوم معمولاً با روش سطح هزینه مرتبط است، که اجازه می‌دهد مسیرهای بهینه از طریق رستر محاسبه شود که در آن ارزش هر سلول هزینه پیمایش از طریق آن سلول را نشان می‌دهد. یکی از مشکلات این روش هزینه محاسباتی است که ممکن است با شطرنجی های بزرگ بسیار زیاد باشد. در این مطالعه، یک روش مسیریابی به نام مسیریابی سلسله مراتبی A* (HPA*)، بر اساس یک استراتژی انتزاعی، به عنوان جایگزینی برای رویکرد سنتی بررسی شده است. هدف از این مطالعه ارتقای روش به منظور مناسب‌تر کردن آن برای محاسبه مسیرها نسبت به رسترهای هزینه با هزینه پیمایش غیریکنواخت است. این روش در GIS پیاده سازی شده و با داده های واقعی تست شده است. نتایج نشان می‌دهد که با در نظر گرفتن اطلاعات تعبیه‌شده در رستر هزینه، مسیرهای با کیفیت نسبتاً خوب را می‌توان محاسبه کرد در حالی که صرفه‌جویی قابل‌توجهی در تلاش محاسباتی در مقایسه با رویکرد سنتی و غیر سلسله‌مراتبی دارد.
کلید واژه ها: 

مسیریابی خارج از شبکه شطرنجی هزینه ; انتزاع سلسله مراتبی

 

1. مقدمه

مسیریابی از طریق شبکه های حمل و نقل به یک فناوری جا افتاده هم در کاربردهای علمی و هم در کاربردهای تجاری تبدیل شده است. این امر در حجم وسیعی از مطالعات مربوط به دسترسی، شبیه سازی ترافیک و مشکلات انتخاب سایت، و همچنین در محبوبیت روزافزون ناوبری خودرو، برنامه ریزی سفر و سیستم های مدیریت ناوگان آشکار می شود. تقاضا برای راه حل های مسیریابی خارج از حوزه شبکه های حمل و نقل نیز وجود دارد، از جمله برنامه های کاربردی مربوط به حرکت و ناوبری در محیط های بین کشوری [ 1 ، 2 ، 3 ] و کاربردهای مربوط به تراز و ساخت سازه های خطی مانند جاده ها، خطوط لوله یا نیرو. خطوط انتقال [ 4 ، 5, 6 , 7 , 8 ].
صرف نظر از حوزه کاربرد، مسیریابی اساساً مبتنی بر نظریه گراف و مفاهیم آن است. یک گراف که معمولاً به عنوان نشان داده می شود

Ijgi 02 00996 i001

شامل مجموعه ای از گره ها (یا رئوس، نقاط) N و مجموعه ای از لبه ها (یا قوس ها، خطوط، پیوندها) E . یک لبه

Ijgi 02 00996 i002

گره‌های i و j را به هم متصل می‌کند و یک هزینه مرتبط با C i,j دارد. هزینه نشان دهنده امپدانس سفر، مانند فاصله یا زمان جغرافیایی، بین i و j است. یک مسیر بهینه و کم هزینه بین هر دو گره از نمودار را می توان با استفاده از الگوریتم جستجوی نمودار محاسبه کرد [ 9 ، 10 ].

تئوری گراف به خوبی می تواند شبکه های حمل و نقل دنیای واقعی را به عنوان نمودارهای تک بعدی نشان دهد، جایی که اتصالات جاده ها به عنوان گره عمل می کنند و جاده ها لبه های نمودار هستند. هزینه های لبه را می توان به راحتی از طول فیزیکی بخش های جاده، یا از زمان تخمینی سفر در امتداد جاده های مختلف به دست آورد. متأسفانه، ریختن فضای خارج از شبکه به یک نمایش مشابه به همان اندازه ساده نیست. اولاً، مناسب بودن انواع مختلف زمین برای سفر اغلب مختص کاربرد است، و شناسایی مقادیر مناسب هزینه پیمایش ممکن است نیاز به مدل‌سازی دانش پرزحمت داشته باشد. ثانیا، و مهمتر از آن، حرکت در فضای خارج از شبکه به جای یک بعد، در دو بعد صورت می گیرد، همانطور که در شبکه های حمل و نقل به طور موثری اتفاق می افتد.

2. GIS و هزینه رستر

در زمینه سیستم های اطلاعات جغرافیایی (GIS)، مسیریابی را می توان با استفاده از ساختار داده بردار یا شطرنجی انجام داد که هر دو دارای نقاط قوت و ضعف مربوطه هستند. در ساختار داده برداری، هر شی از یک سری جفت مختصات تشکیل شده است. این ساختار داده برای یافتن مسیرها در موقعیت هایی که محیط از موجودیت هایی با مرزهای کاملاً مشخص تشکیل شده است بسیار مفید است. با این حال، اغلب وظیفه تعیین مسیرها از طریق فضای خارج از شبکه مبتنی بر ایده تجزیه و تحلیل سطح هزینه است که در آن فضا توسط سلول های گسسته و منظم به طور خاص مرتبط با ساختار داده شطرنجی نشان داده می شود. مزایای اصلی ساختار شطرنجی این است که به دلیل ترکیب منظم آنها، رسترها به راحتی قابل پردازش و پردازش هستند.11 ، 12 ، 13 ].
یک نمایش شطرنجی از فضا را می توان با در نظر گرفتن نقطه مرکزی هر سلول به عنوان یک گره و اتصال هر نقطه به نقاط مرکزی سلول های دیگر به یک نمودار تبدیل کرد. از آنجایی که تعداد بی نهایت گزینه حرکت در فضای دو بعدی وجود دارد، راه های متعددی نیز برای تقریبی اتصال وجود دارد. متداول ترین الگوی اتصال استفاده شده، پیوند دادن یک سلول به چهار همسایه متعامد و چهار همسایه مورب آن است که معادل هشت زاویه حرکت است [ 14 ]. البته می‌توان همسایگی را فراتر از همسایه‌های همجوار گسترش داد و جهت‌های حرکتی بیشتری را امکان‌پذیر کرد، اما منجر به یک نمودار متراکم فزاینده می‌شود [ 15 ، 16 ]]. اگر سلول های شطرنجی با مقادیر هزینه تخصیص داده شوند (تعریف هزینه حرکت به ازای واحد فاصله از طریق سلول)، هزینه هر مرحله که مرکز دو سلول را به هم متصل می کند را می توان با توجه به کشش مسافت طی شده از طریق سلول های زیرین محاسبه کرد. [ 17 ].
نمودار شطرنجی اجازه می دهد تا از الگوریتم های مشابهی که معمولاً در شبکه های حمل و نقل استفاده می شود در محاسبه مسیرهای فضای خارج از شبکه استفاده شود. به طور معمول الگوریتم کلاسیک که در اصل توسط Dijkstra [ 18 ] پیشنهاد شده بود، یا گونه‌ای از آن، برای این منظور استفاده می‌شود. الگوریتم دایکسترا در ادبیات شناخته شده است و تقریباً در هر کتابی در مورد الگوریتم ها یافت می شود (برای مثال، [ 19 ] را ببینید).
الگوریتم Dijkstra اساساً مسئله مسیرهای کم‌هزینه تک منبع را در نمودار وزنی G حل می‌کند . به عبارت دیگر، درختی از مسیرهای کم‌هزینه از یک گره شروع s تا تمام گره‌های دیگر G تولید می‌کند. الگوریتم با تخصیص یک مقدار هزینه آزمایشی c به همه گره ها راه اندازی می شود: صفر برای s و بی نهایت برای همه گره های دیگر. در مرحله اولیه، همه گره‌ها با علامت “باز” ​​مشخص می‌شوند که نشان می‌دهد هنوز توسط الگوریتم بازدید نشده است. سپس الگوریتم به طور مکرر گرهی را با کوچکترین c در میان گره های «باز» انتخاب و «بسط» می کند. این بدان معنی است که الگوریتم تمام همسایگان بازدید نشده i را اسکن می کند، و بررسی می کند که آیا مقدار ترکیبی c i و هزینه لبه اتصال i و همسایه آن j کوچکتر از مقدار آزمایشی ثبت شده قبلی c j است. اگر چنین باشد، c j با مقدار جدید و کوچکتر به روز می شود. هنگامی که همه همسایگان i پردازش شدند، i “بسته” علامت گذاری می شود و بنابراین دیگر توسط الگوریتم بازدید نمی شود. این فرآیند تا زمانی تکرار می شود که تمام گره های قابل دسترسی از s بازدید شوند، یا اگر باید مسیری بین s و گره مقصد d پیدا شود (به جای sبرای تمام گره های دیگر)، کافی است به محض رسیدن به d ، جستجو را خاتمه دهید. مسیر بین دو گره را می توان به سادگی با پشت سر گذاشتن دنباله حرکت از d به s تعیین کرد، که فقط مستلزم آن است که یک اشاره گر به گره قبلی توسط الگوریتم به هر گره اختصاص داده شود.
زمان اجرای الگوریتم دایکسترا در ابتدایی ترین شکل آن است

Ijgi 02 00996 i003

که در آن N و E به ترتیب نشان دهنده تعداد گره ها و لبه ها هستند. با این حال، زمانی که الگوریتم با یک صف اولویت برای بازیابی سریع ارزان‌ترین گره فعلی پیاده‌سازی می‌شود، زمان اجرا به کاهش می‌یابد.

Ijgi 02 00996 i004

با فرض اینکه صف به صورت یک پشته باینری پیاده سازی شده است.

3. استراتژی هایی برای بهبود مسیریابی مبتنی بر شطرنجی

دو اشکال عمده در مسیریابی مبتنی بر شطرنجی وجود دارد: یکی اعوجاج ذاتاً در مسیرهای مبتنی بر شطرنجی، و دیگری تلاش محاسباتی زیاد مورد نیاز برای محاسبه مسیرها، به ویژه هنگامی که به شطرنجی های بزرگ مربوط می شود. اعوجاج ناشی از الگوی همسایگی مورد استفاده برای ایجاد نمودار شطرنجی، خود را به عنوان خطای کشیدگی و انحراف نشان می دهد. خطای ازدیاد طول به این دلیل است که مسیر مبتنی بر شطرنجی به طور اجتناب‌ناپذیری از یک مرکز سلول به مرکز یکی از سلول‌های مجاور پیش می‌رود. بر این اساس، بین فاصله اندازه‌گیری شده در فضای شطرنجی و فضای پیوسته اختلاف وجود دارد: اولی بیشتر از دومی است. خطای انحراف، به نوبه خود، فاصله مسیر شطرنجی از مسیر فضای پیوسته مربوطه است.15 ].
استفاده از محله های بزرگتر یک استراتژی مرسوم برای کاهش اعوجاج در مسیرهای ناشی از ساختار شطرنجی است. به جای الگوی مرسوم هشت متصل، الگوهای بزرگتری که 16، 32 یا حتی بیشتر همسایه را در بر می گیرند استفاده شده است [ 14 ، 15 ، 16 ، 20 ]. حتی اگر اعوجاج را می توان به این روش کاهش داد، با هزینه نمودارهای متراکم فزاینده و هزینه محاسباتی مرتبط همراه است. راه دیگر برای پرداختن به مشکل، تصحیح مسیرهای محاسبه شده با جایگزینی بخش های تحریف شده مسیر با خطوط مستقیم، در صورت امکان است [ 20 ، 21 ]. این منجر به شهود بیشتر و همچنین مسیرهای مفیدتر می شود.
اشکال عمده دیگر مسیریابی مبتنی بر شطرنجی – هزینه محاسباتی بالا – یک چالش کلی در مورد انواع مشکلات جستجوی نمودار است. با این حال، این مشکل برای نمودارهای مبتنی بر شطرنجی به دلیل چگالی بالای آنها تشدید می شود. یک رستر معمولاً باید وضوح نسبتاً بالایی داشته باشد تا بتواند نمایش دقیقی از محیط ارائه دهد. همانطور که هر سلول به عنوان یک گره در نظر گرفته می شود، این به تعداد زیادی گره در نمودار تبدیل می شود. در مقابل، برای نمودارهایی که شبکه‌های حمل و نقل را نشان می‌دهند، تعداد نسبتاً کمی از گره‌ها برای نمایش شبکه مورد نیاز است که هر گره معمولاً فقط به دو یا سه گره متصل است.
اگرچه الگوریتم Dijkstra به ندرت در شکل اصلی خود بدون استفاده از ساختارهای داده داخلی کارآمدتر مورد استفاده قرار می گیرد، با این وجود یافتن مسیری با الگوریتم Dijkstra از نظر محاسباتی، به ویژه با نمودارهای بزرگ، سخت است. کارایی محاسباتی مسیریابی را می توان با استراتژی های اکتشافی بهبود بخشید، که می توانند به سه دسته طبقه بندی شوند: محدود کردن منطقه جستجو، تجزیه مشکل جستجو، و استفاده از یک استراتژی حل مسئله “انتزاعی” [ 22 ].]. ایده محدود کردن منطقه جستجو استفاده از دانش در مورد مکان های شروع و مقصد برای محدود کردن جستجو به یک مسیر کم هزینه در یک منطقه خاص است. این به یکی از معایب اصلی الگوریتم Dijkstra می پردازد، یعنی اینکه جستجو را به جای جهت واقعی مقصد، در همه جهات منتشر می کند. الگوریتم A* که در اصل توسط هارت و همکاران ارائه شد. [ 23 ]، معمولاً برای رسیدگی به این مشکل استفاده می شود. Dijkstra و A* به طور موثر مشابه هستند، با این استثنا که دومی یک جستجوی آگاهانه را بر اساس یک تابع ارزیابی اکتشافی انجام می دهد. تابع به صورت مشخص شده است

Ijgi 02 00996 i005

که در آن g(n) هزینه مسیر از s به n را می دهد و h(n) هزینه تخمینی برای رسیدن از n به d است [ 24 ]. اگر تخمین اکتشافی استفاده شده توسط الگوریتم قابل قبول باشد، به این معنی که فاصله n تا d هرگز بیش از حد تخمین زده نمی شود، الگوریتم تضمین می شود که مسیر بهینه را پیدا کند [ 25 ]]. A* به عنوان بهترین انتخاب در کلاس الگوریتم های خود در نظر گرفته می شود: هیچ الگوریتم بهینه دیگری برای گسترش گره های کمتر از A* تضمین نمی شود. با این حال، این همیشه جستجوی سریع را تضمین نمی کند، زیرا برای اکثر مشکلات، تعداد گره ها در فضای جستجو همچنان در طول مسیر نمایی است [ 24 ].

هر دو Dijkstra و A* الگوریتم های قطعی هستند که از قوانین خاصی در عملکرد خود پیروی می کنند و بنابراین رفتار آنها کاملاً قابل پیش بینی است [ 26 ]. به عنوان جایگزینی برای این روش‌ها، روش‌های تصادفی با استفاده از قوانین جستجوی احتمالی برای حل مسائل مسیریابی استفاده شده‌اند. به عنوان مثال، بهینه سازی کلونی مورچه ها (ACO)، با الهام از رفتار مورچه ها [ 27 ]، برای یافتن مسیرهای بهینه در تصاویر زمین [ 28 ] و در محیط های داخلی [ 29 ] استفاده شده است. الگوریتم‌های ژنتیک (GA)، با تکیه بر اصول انتخاب طبیعی [ 30 ]، همچنین برای رسیدگی به کوتاه‌ترین مسیر [ 31 ]، مکان راهرو [ 32 ] و مشکلات مسیریابی مجدد [30] استفاده شده است.33 ]. با توجه به ارزیابی عملکرد Dijkstra، A* و GA [ 26 ]، استفاده از یک روش جستجوی تصادفی می تواند انتخاب کارآمدتری در مقایسه با روش های قطعی، به ویژه برای مشکلات مسیریابی در مقیاس بزرگ باشد. با این حال، به دلیل قابل پیش بینی بودن و قابل پیش بینی بودن روش های قطعی، این احتمال وجود دارد که به ویژه A* یک انتخاب محبوب برای مسیریابی باقی بماند، مشروط بر اینکه بتوان از تکنیک هایی برای بهبود عملکرد آن استفاده کرد.
جستجوی دوطرفه، که به دسته تکنیک‌هایی با هدف تجزیه مشکل جستجو تعلق دارد، یکی از گزینه‌های موجود برای محدود کردن تلاش جستجوی الگوریتم A* است. در این تکنیک، دو جستجو به طور همزمان انجام می شود: یکی از s به سمت d و دیگری در جهت مخالف. یک مسیر بهینه زمانی پیدا می شود که این دو جستجو در جایی در وسط یکدیگر را ملاقات کنند. منطق استفاده از جستجوی دو طرفه به جای یک طرفه این است که در حالی که یک درخت جستجو به صورت تصاعدی بر اساس عمق خود رشد می کند، تعداد ترکیبی از گره های پردازش شده توسط دو جستجوی کوچکتر می تواند حداقل در اصل کمتر از تعداد گره های پردازش شده توسط یک جستجوی بزرگ باشد. جستجو [ 34 ، 35 ، 36]. چالش با جستجوی دوطرفه این است که هیچ تضمینی وجود ندارد که یک مسیر بهینه بین s و d در هنگام برخورد دو مرز جستجو پیدا شود. بنابراین ممکن است مرزهای جستجو به طور قابل توجهی با یکدیگر همپوشانی داشته باشند و در نتیجه عملکردی پایین تر از جستجوی یک طرفه معمولی داشته باشند. در حالی که چندین راه حل برای ارائه کارایی بهبود یافته در مقایسه با جستجوی دوسویه مرسوم تر [ 36 ، 37 ، 38 ] پیشنهاد شده است، کاربرد آنها به طور گسترده با مجموعه داده های دنیای واقعی آزمایش نشده است [ 22 ].
اگرچه فرآیند جستجوی نمودار را می توان با استفاده از تکنیک های شرح داده شده در بالا کوتاه کرد، اما آنها همیشه راه حل رضایت بخشی برای چالش محاسباتی ایجاد شده توسط نمودارهای بزرگ ارائه نمی دهند. بنابراین، به جای تلاش برای اصلاح الگوریتم جستجو، یک راه جایگزین برای جستجوی عملکرد بهبود یافته، کاهش اندازه نمودار است. این ممکن است شامل ایجاد یک انتزاع از مشکل، در نتیجه حفظ تنها ویژگی های اساسی مسئله و کنار گذاشتن جزئیات نامربوط باشد. برای رسترها و نمودارهای شطرنجی، چندین تکنیک استاندارد وجود دارد که ممکن است برای ایجاد یک انتزاع استفاده شود. ساده ترین راه این است که وضوح شطرنجی را با استفاده از نمونه برداری مجدد کاهش دهیم و سپس از رستر درشت برای ساختن نمودار شطرنجی استفاده کنیم. در حالی که این ممکن است در واقع منجر به کاهش چشمگیر در اندازه نمودار شطرنجی و زمان محاسبه شود، اشکال آشکار آن از دست دادن اطلاعات و جزئیات است. یک مشکل به طور خاص مربوط به موانع و گذرگاه‌های باریکی است که توسط موانع احاطه شده‌اند، که ممکن است در قطعنامه‌های درشت کاملاً از بین بروند. در نتیجه، روش مسیریابی ممکن است نتواند هیچ مسیری را بیابد (حتی اگر در واقعیت وجود داشته باشد)، یا ممکن است مسیری را از طریق یک منطقه غیرقابل دسترس پیشنهاد کند. این مشکل را می توان با تبدیل شطرنجی به یک نمایش چهار درختی [ روش مسیریابی ممکن است نتواند هیچ مسیری را بیابد (حتی اگر در واقعیت وجود داشته باشد)، یا ممکن است مسیری را از طریق یک منطقه غیرقابل دسترس پیشنهاد کند. این مشکل را می توان با تبدیل شطرنجی به یک نمایش چهار درختی [ روش مسیریابی ممکن است نتواند هیچ مسیری را بیابد (حتی اگر در واقعیت وجود داشته باشد)، یا ممکن است مسیری را از طریق یک منطقه غیرقابل دسترس پیشنهاد کند. این مشکل را می توان با تبدیل شطرنجی به یک نمایش چهار درختی [39 ] که در آن گروهی از سلول‌ها، مرحله به مرحله، به چهار گروه کوچک‌تر تقسیم می‌شوند تا زمانی که هر ربع به یک بلوک یکنواخت از سلول‌ها مطابقت داشته باشد. در مقایسه با استفاده از شطرنجی اصلی برای مسیریابی، جستجوی چهاردرختی برای مسیر بهینه ممکن است به طور قابل ملاحظه‌ای سریع‌تر باشد، زیرا تعداد سلول‌ها (گره‌ها) به طور بالقوه به طور قابل توجهی در نمایش چهاردرخت کمتر است [ 40 ]. با این حال، این رویکرد ممکن است زمانی که سلول‌ها بزرگ هستند، نتایج کمتر از حد بهینه را به همراه داشته باشد، که نیاز به پس پردازش مسیرها، استفاده از درخت‌های چهارگانه «قاب‌بندی‌شده» یا استراتژی‌های جایگزینی قرار دادن گره دارد [ 16 ، 20 ، 41 ].
یک راه حل رایج برای ایجاد انتزاعات، به ویژه در زمینه شبکه های حمل و نقل، بهره برداری از سلسله مراتب است. یکی از گزینه ها استفاده از سلسله مراتب طبیعی موجود در شبکه های حمل و نقل است. با ترجیح جاده های اولیه و بی توجهی به جزئیات محلی نامربوط، زمان محاسبه را می توان به طور قابل توجهی کاهش داد. سلسله مراتب همچنین ممکن است به مجموعه ای از انتزاعات متوالی شبکه اشاره داشته باشد که به طور خاص برای اهداف مسیریابی ایجاد شده اند. مکانیسم های زیادی برای ایجاد چنین انتزاعی هایی وجود دارد، همانطور که در بررسی استورتوانت و یانسن [ 42 ] توضیح داده شد.]. در حالی که تکنیک‌های خاصی مانند سلسله مراتب مبتنی بر دسته، برای نمودارهای عمومی که در آن روابط توپولوژیکی گره‌ها به صراحت تعریف شده است، مناسب‌تر هستند، به اصطلاح سلسله‌مراتب مبتنی بر بخش به ویژه برای نمودارهای شطرنجی مفید است، جایی که روابط توپولوژیکی ضمنی هستند و یک ساختار منظم را به تصویر بکشید.
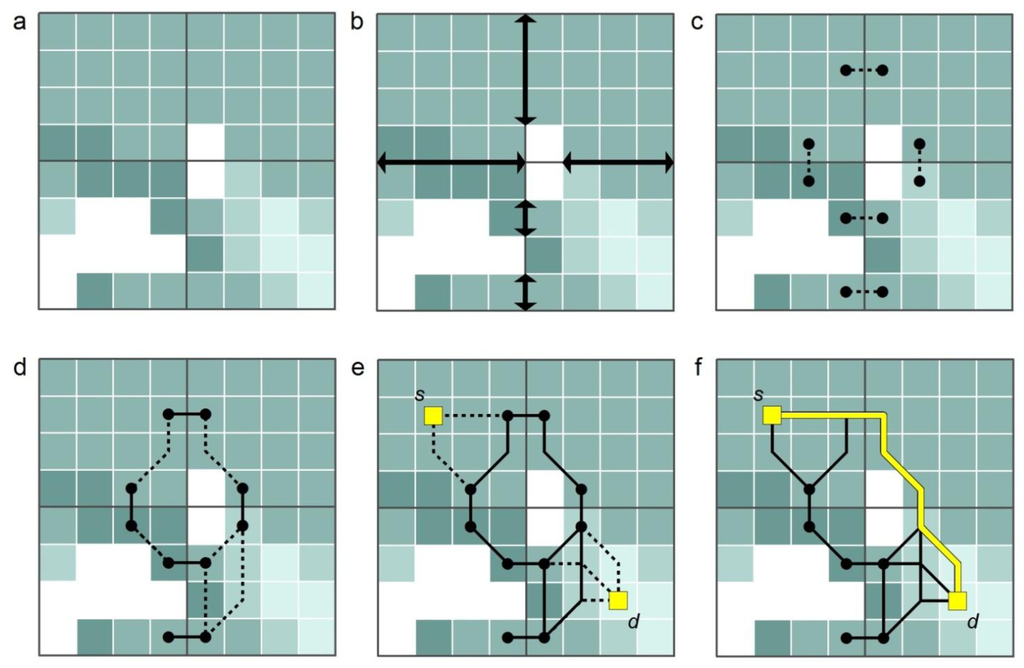
مسیریابی سلسله مراتبی A* (HPA*)، پیشنهاد شده توسط Botea و همکاران. [ 43 ] و توسط Jansen و Buro [ 44 ] و Harabor و Botea [ 45 ] بهبود یافته است، یک روش مسیریابی است که شامل دو استراتژی اکتشافی (الگوریتم A* و یک استراتژی انتزاعی) برای بهبود عملکرد محاسباتی مسیریابی مبتنی بر شطرنجی است. . ایده اساسی ایجاد یک انتزاع در روش HPA* مبتنی بر تقسیم یک رستر به مجموعه‌ای از بلوک‌های با اندازه مساوی است (یا همانطور که لی و همکاران [ 46 ] پیشنهاد می‌کنند به بلوک‌هایی با اندازه نامنظم بر اساس درخت تصمیم). این مرحله اولیه در شکل 1 نشان داده شده استآ. سپس، برای هر مرز بین دو بلوک مجاور، بخش‌های بدون مانع در امتداد مرز مشخص می‌شوند ( شکل 1 ب). این بخش ها ورودی های بین بلوک ها هستند. حرکت از طریق ورودی فقط از طریق انتقال مجاز است ، که برای هر ورودی با توجه به یک طرح قرارگیری انتقال از پیش تعیین شده تعریف شده است. یک انتقال شامل دو گره است که هر کدام در یک طرف مرز بین دو بلوک مجاور قرار می گیرند. یک لبه بین این گره های مرزی کشیده می شود و بلوک ها را به هم متصل می کند ( شکل 1ج). لبه های این نوع “بین لبه” نامیده می شود. نوع دیگری از یال‌ها، «داخل لبه‌ها»، بین تمام جفت‌های گره‌های مرزی در هر بلوک با محاسبه مسیرهای کم‌هزینه بین آن‌ها با استفاده از هشت اتصال تعریف می‌شوند ( شکل 1 د). گره های مرزی، همراه با دو نوع یال، نمودار را در سطح پارتیشن بلوک تشکیل می دهند. بدیهی است که قبل از استفاده از نمودار برای محاسبه مسیر بین مکان‌های s و d (که ممکن است در هر نقطه‌ای از شطرنجی قرار گیرند) این مکان‌ها باید به طور موقت به نمودار متصل شوند. این کار با محاسبه مسیرهای کم‌هزینه از s به گره‌های مرزی بلوک حاوی s و تکرار همین روش برای d نیز انجام می‌شود.شکل 1 ه). در نهایت، یک مسیر بین s و d را می توان بر روی نمودار با استفاده از الگوریتم A* محاسبه کرد ( شکل 1 f).
کاربرد HPA* این است که محاسبات زیادی را می توان در مرحله پیش پردازش انجام داد (فازهای a-d در شکل 1 )، که کار مسیریابی واقعی را بسیار سریعتر می کند. هنگامی که یک مسیر بین مکان‌های s و d درخواست می‌شود ، تنها چیزی که نیاز است این است که به طور موقت آنها را با انجام جستجوهای کوچک Dijkstra بر روی رستر هزینه اصلی در بلوک‌های حاوی s و d به نمودار از پیش محاسبه‌شده متصل کنید و سپس یک مسیر بین آنها را محاسبه کنید. نمودار با استفاده از A*.
تلاش محاسباتی کلی فاز مسیریابی با اندازه بلوک تعیین می شود. اندازه بلوک بزرگ به یک نمودار سبک وزن با تعداد نسبتاً کمی گره ترجمه می شود. این باعث صرفه جویی در زمان در مرحله مسیریابی می شود، اما نقطه ضعف اندازه بلوک بزرگ، افزایش تلاش مورد نیاز برای اتصال s و d است.به نمودار برعکس، اندازه بلوک کوچک زمان مورد نیاز برای اتصال مکان‌ها به نمودار را کاهش می‌دهد، اما خود نمودار شامل گره‌های بیشتری خواهد بود، بنابراین هزینه محاسباتی افزایش می‌یابد. به منظور پرداختن به این مشکل مبادله، می توان یک نمودار چند سطحی ساخت. مزیت یک نمودار چند سطحی این است که امکان محاسبه سریع مسیرها با استفاده از سطوح انتزاعی بالا را فراهم می کند، در حالی که سطح پایه ای از بلوک های کوچک را فراهم می کند که از نیاز به انجام جستجوهای بزرگ در شطرنج اصلی برای اتصال s و d جلوگیری می کند. به نمودار
علاوه بر اندازه بلوک، الگوی قرارگیری انتقال ها پارامتر مهمی است که بر کیفیت مسیرهای تولید شده توسط روش تأثیر می گذارد. در مطالعه خود، Botea و همکاران. [ 43اگر عرض ورودی کمتر از شش خانه باشد، انتقال را در وسط ورودی قرار دهید. در غیر این صورت، دو انتقال تعریف شده است، یکی در هر انتهای ورودی. توجه به این نکته حائز اهمیت است که این الگوی قرارگیری برای شطرنج‌های باینری استفاده می‌شود که فقط از فضای آزاد با هزینه عبور یکنواخت و موانع غیرقابل عبور تشکیل شده‌اند. برای شطرنج‌های این نوع، موقعیت انتقال‌ها عامل بسیار مهمی نیست، زیرا مسیرهای محاسبه‌شده را می‌توان بعداً با جایگزینی بخش‌های منحنی غیرضروری مسیرها با خطوط میانبر مستقیم تصحیح کرد، مشروط بر اینکه میانبرها هیچ مانعی را قطع نکنند. با این حال، بیشتر مجموعه داده‌های دنیای واقعی طیف گسترده‌ای از شرایط قابل عبور را شامل می‌شوند که نمی‌توان آن را به دو کلاس کاهش داد. در چنین موردی، یک استراتژی قرار دادن انتقال مبتنی بر فرض تقسیم دوتایی فضا ممکن است چندان مفید نباشد. این اولاً درست است زیرا بدون در نظر گرفتن هزینه پیمایش اساسی، انتقال ممکن است در موقعیتی قرار گیرد که به ندرت توسط هر مسیر واقعاً بهینه استفاده می شود. ثانیاً، با توجه به هزینه‌های متفاوت سلول‌ها، مسیرها را نمی‌توان با جایگزینی بخش‌های منحنی مسیر با میانبرهای مستقیم در مرحله پس پردازش بهبود بخشید. به عبارت دیگر، انتقال ها باید در وهله اول در مناسب ترین مکان ها قرار گیرند، زیرا هم ترازی مسیر نمی تواند بعداً به طور موثر بهبود یابد. انتقال ممکن است در نهایت در موقعیتی قرار گیرد که به ندرت توسط هر مسیر واقعاً بهینه استفاده می شود. ثانیاً، با توجه به هزینه‌های متفاوت سلول‌ها، مسیرها را نمی‌توان با جایگزینی بخش‌های منحنی مسیر با میانبرهای مستقیم در مرحله پس پردازش بهبود بخشید. به عبارت دیگر، انتقال ها باید در وهله اول در مناسب ترین مکان ها قرار گیرند، زیرا هم ترازی مسیر نمی تواند بعداً به طور موثر بهبود یابد. انتقال ممکن است در نهایت در موقعیتی قرار گیرد که به ندرت توسط هر مسیر واقعاً بهینه استفاده می شود. ثانیاً، با توجه به هزینه‌های متفاوت سلول‌ها، مسیرها را نمی‌توان با جایگزینی بخش‌های منحنی مسیر با میانبرهای مستقیم در مرحله پس پردازش بهبود بخشید. به عبارت دیگر، انتقال ها باید در وهله اول در مناسب ترین مکان ها قرار گیرند، زیرا هم ترازی مسیر نمی تواند بعداً به طور موثر بهبود یابد.
Ijgi 02 00996 g001 1024
شکل 1. طرح روش HPA*: ( الف ) تقسیم هزینه به بلوک ها، ( ب ) شناسایی ورودی ها در امتداد مرزهای بلوک، ( ج ) تعیین یک انتقال (بین لبه) برای نشان دادن هر ورودی، ( d) ) اتصال گره های انتقال در هر بلوک (داخل یال ها)، ( e ) اتصال s (شروع) و d (مقصد) به طور موقت به نمودار، و ( f ) یافتن مسیری بین s و d .
اگرچه روش HPA* و به طور کلی مسیریابی مبتنی بر شطرنجی به طور گسترده در ادبیات مطالعه شده است، اما بیشتر تحقیقات در زمینه های رباتیک، تحقیقات عملیاتی و بازی های رایانه ای انجام شده است. در این زمینه‌ها، معمولاً بر مشکلات اجتناب از موانع در محیط‌های محدود تأکید می‌شود، در حالی که در جغرافیا و GIS، مسیریابی معمولاً شامل هزینه‌های پیمایش متنوع و مناطق جغرافیایی بزرگ است. با این حال، روش استاندارد مسیریابی مبتنی بر شطرنجی، صرف نظر از محدودیت‌های آن، معمولاً بدون در نظر گرفتن روش‌های جایگزین در GIS استفاده می‌شود.
با انگیزه فقدان آشکار تحقیق، سهم مورد نظر از این مطالعه پیشنهاد بهبود الگوریتم HPA* است که اجازه می‌دهد انتقال‌ها به شیوه‌ای آگاهانه‌تر از آنچه در مطالعات قبلی پیشنهاد شده است قرار گیرند. سپس کل الگوریتم پیشنهادی در GIS پیاده سازی شده و با داده های واقعی آزمایش و ارزیابی می شود. سهم این مطالعه باید برای جغرافیا و GIS و مناطق کاربردی مرتبط که در آن مسیرها باید از نظر هزینه پیمایش متغیر بهینه شوند، مورد توجه خاص قرار گیرد.

4. روش اجرا

اجرای آزمایشی روش HPA* با استفاده از زبان برنامه نویسی C# و اجزای ArcObjects نرم افزار ArcGIS برای این مطالعه انجام شد. الگوریتم اصلی HPA*، همراه با شبه کد آن، به تفصیل در [ 43 ] توضیح داده شده است و در اینجا تکرار نخواهد شد. بخش‌های عمده روش اجرا شده و سهم این کار، در زیر توضیح داده شده است.

4.1. استراتژی های جایابی انتقالی

همانطور که در بالا توضیح داده شد، انتقال ها نقش مهمی در روش HPA* دارند. از آنجایی که دسترسی از یک بلوک به بلوک دیگر تنها از طریق انتقال مجاز است، و از آنجایی که مسیرهای بین هر شروع و مقصدی باید آنها را به اشتراک بگذارند، انتقال ها به شدت بر کیفیت مسیرها تأثیر می گذارد. سه استراتژی مختلف برای قرار دادن یک انتقال در ورودی به روش HPA* در این مطالعه در نظر گرفته شده است. این استراتژی ها بر اساس ایده قرار دادن یک انتقال یا در وسط ورودی، با کمترین هزینه، یا در موقعیت بهترین دسترسی هستند و به عنوان مخفف های یک حرفی، M، C، و نامیده می شوند. الف به ترتیب.
استراتژی M به طور مستقیم از Botea و همکاران اتخاذ شده است. [ 43 ]. با وجود ساده بودن، مزایای خاصی دارد. اولین مزیت، قابلیت حمل و نقل آن است: هیچ ارزیابی پیچیده ای از هزینه های سلولی لازم نیست انجام شود. ثانیاً، انتقالی که در وسط ورودی قرار می‌گیرد می‌تواند در به حداقل رساندن خطای احتمالی نسبتاً کارآمد باشد، به‌ویژه زمانی که هزینه اساسی در کل عرض ورودی یکنواخت باشد.
نقص استراتژی M در این واقعیت نهفته است که مسیرهای بهینه به نفع مناطق با هزینه رفت و آمد کم، به ویژه راهروهای کم هزینه هستند. استراتژی M این را در نظر نمی گیرد، و بنابراین احتمال زیادی وجود دارد که مکان انتقال از مکان هایی که مسیرهای واقعا بهینه از مرز بلوک عبور می کنند، منحرف شود. در مقابل، استراتژی C با هدف قرار دادن انتقال در موقعیتی با کمترین هزینه پیمایش در امتداد ورودی است. این روش به طور قابل توجهی پیچیده تر از روش M نیست زیرا فقط هزینه سلول های دو طرف ورودی باید ارزیابی شود. این سادگی، باز هم، نقطه ضعف آن است. موقعیت با کمترین هزینه انتقال در امتداد مرز ممکن است تنها یک مورد مجزا یا بخشی از یک خوشه محلی از سلول های کم هزینه باشد نه یک منطقه بزرگتر یا راهرو با هزینه عبور کم. به خصوص گروه‌های محلی سلول‌های کم‌هزینه در نزدیکی هر دو انتهای ورودی مشکل‌ساز هستند، زیرا ممکن است مسیرها را مجبور به پیچش‌های غیرضروری کند و در نتیجه کیفیت مسیر را مختل کند.
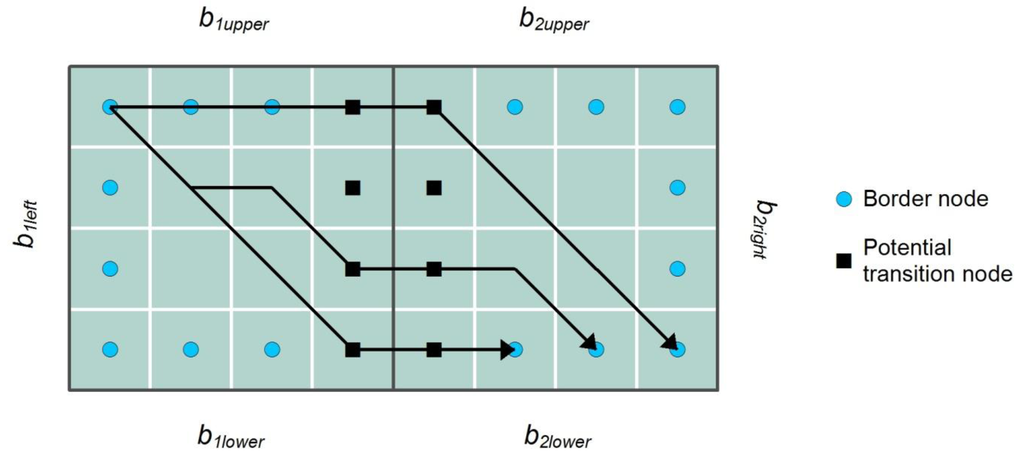
محدودیت‌های استراتژی‌های M و C را می‌توان با سومین استراتژی قرار دادن انتقال ارائه شده در اینجا، یعنی استراتژی مبتنی بر تعیین مکان بهترین دسترسی (A) مورد بررسی قرار داد. هدف استراتژی A این است که با دقت بیشتری پیش بینی کند که مسیرهایی که از یک بلوک به یک بلوک مجاور عبور می کنند از یک ورودی بین این دو عبور می کنند. در اینجا، دسترسی به طور کلی به هزینه کلی حرکت بین یک نامزد انتقال در مرز بین دو بلوک و سایر مرزهای بلوک اشاره دارد. روش های مختلفی برای ارزیابی قابلیت دسترسی یک نامزد انتقالی وجود دارد. یکی از ساده ترین گزینه ها محاسبه مسیرهای کم هزینه از هر دو گره است که شامل انتقال به سلول های مرزی بلوک های مربوطه می شود و سپس از این اطلاعات برای تعیین امتیاز دسترسی استفاده می شود. مشکل این رویکرد این است که مکان‌ها در وسط مرز بلوک به طور طبیعی امتیازهای دسترسی بالایی را دریافت می‌کنند، و در نتیجه الگوی قرار دادن انتقال A شبیه M است که منجر به یک انتزاع اساساً مشابه می‌شود. بنابراین، برای تعیین امتیاز دسترسی باید یک استراتژی متفاوت اتخاذ شود. ایده این است که تخمین بزنیم که مسیرهای کم‌هزینه عبور از یک بلوک به بلوک دیگر به احتمال زیاد از مرز بین این دو عبور می‌کنند. برای تعیین این، مسیرهای کم‌هزینه بین سلول‌های لبه‌های بلوک “مقابل” برای هر جفت بلوک مجاور که یک مرز مشترک دارند محاسبه می‌شوند. این در نشان داده شده استشکل 2 برای بلوک های افقی مجاور، B 1 و B 2 ، با اندازه 4 × 4 سلول. این روش بین تمام جفت سلول ها در امتداد مرزهای b 1بالا و b 2پایین ، b 1پایین و b 2بالا و b 1چپ و b 2 راست انجام می شود.، بدون احتساب سلول هایی که نقش یک گره انتقال بالقوه را اختصاص داده اند. هنگامی که تمام مسیرهای متصل کننده سلول ها در مرزهای مخالف بلوک ها محاسبه شد، امتیاز دسترسی برای هر گره انتقال بالقوه با جمع کردن تعداد مسیرهایی که از هر گره عبور می کنند تعیین می شود. انتقال بین گره هایی ایجاد می شود که بالاترین امتیاز دسترسی ترکیبی را دارند. اگر دو یا چند انتقال بالقوه در امتداد یک ورودی امتیاز یکسانی داشته باشند، مرکزی ترین این نامزدها به عنوان انتقال عمل می کند.
Ijgi 02 00996 g002 1024
شکل 2. اصل مورد استفاده برای تعیین امتیاز دسترسی. برای اهداف تصویری، مسیرها فقط بین سلول مرزی در گوشه سمت چپ بالای بلوک اول و سلول‌هایی در امتداد مرز مقابل و پایین بلوک همسایه نشان داده می‌شوند. امتیاز محاسبه‌شده، انتقال‌های بالقوه‌ای را نشان می‌دهد که به احتمال زیاد توسط مسیرهای مختلف مشترک خواهد بود، و انتقال در موقعیت بالاترین امتیاز قرار می‌گیرد (در صورت تساوی، مرکزی‌ترین نامزد انتخاب می‌شود).

4.2. انتزاع سلسله مراتبی

علاوه بر قرار دادن انتقال ها، عملکرد روش بیشتر به انتخاب اندازه بلوک و تعداد سطوح سلسله مراتبی بالاتر از سطح پایه بستگی دارد. روش پیاده سازی شده هر دوی این پارامترها را به عنوان ورودی کاربر دریافت می کند. ابتدا، شطرنجی با توجه به اندازه بلوک پایه مشخص شده به بلوک ها تقسیم می شود (به عنوان مثال، 20 × 20 سلول). با استفاده از این تقسیم، انتقال ها بر روی ورودی های بین بلوک های مجاور قرار می گیرند و نمودار ساخته می شود.
اگر سلسله مراتب فقط از سطح پایه L 1 تشکیل شده باشد، این تنها کاری است که باید در مرحله پیش پردازش انجام شود. هنگامی که بیش از یک سطح سلسله مراتبی درخواست می شود، سطوح بر اساس ساختار چهار درختی ساخته می شوند به طوری که هر بلوک در سطح بالاتر از چهار بلوک در یک سطح زیر تشکیل می شود. به عنوان مثال، با اندازه بلوک پایه 20 × 20 سلول و تعداد سطوح تنظیم شده روی سه، اندازه بلوک سطوح L 1 ، L 2 و L 3به ترتیب 20 × 20، 40 × 40 و 80 × 80 سلول خواهد بود. سطوح بالاتر همیشه در بالای نمودار تعریف شده در سطح پایه ساخته می شوند و گره ها و لبه های یکسانی دارند. با این حال، درون لبه‌های بلوک‌های بزرگ‌تر با الحاق لبه‌های سطح پایین‌تر برای ایجاد اتصالات مستقیم بین گره‌های مرزی ساخته می‌شوند. این روش تضمین می کند که در حین تولید انتزاعات سطح بالاتر، کیفیت مسیر تحت تأثیر تعداد سطوح سلسله مراتبی تعریف شده در بالای سطح پایه قرار نمی گیرد. شایان ذکر است که ساختار چهاردرختی مورد استفاده در اینجا به هیچ وجه تنها گزینه قابل تصور برای ساخت سلسله مراتب سلسله مراتبی نیست. ساختار چهار درختی از آنجایی انتخاب شد که در ادبیات به خوبی شناخته شده است و پیاده سازی و مدیریت آن آسان است.
اگر سلسله مراتب فقط از سطح پایه L 1 تشکیل شده باشد، این تنها کاری است که باید در مرحله پیش پردازش انجام شود. هنگامی که بیش از یک سطح سلسله مراتبی درخواست می شود، سطوح بر اساس ساختار چهار درختی ساخته می شوند به طوری که هر بلوک در سطح بالاتر از چهار بلوک در یک سطح زیر تشکیل می شود. به عنوان مثال، با اندازه بلوک پایه 20 × 20 سلول و تعداد سطوح تنظیم شده روی سه، اندازه بلوک سطوح L 1 ، L 1 و L 1به ترتیب 20 × 20، 40 × 40 و 80 × 80 سلول خواهد بود. سطوح بالاتر همیشه در بالای نمودار تعریف شده در سطح پایه ساخته می شوند و گره ها و لبه های یکسانی دارند. با این حال، درون لبه‌های بلوک‌های بزرگ‌تر با الحاق لبه‌های سطح پایین‌تر برای ایجاد اتصالات مستقیم بین گره‌های مرزی ساخته می‌شوند. این روش تضمین می کند که در حین تولید انتزاعات سطح بالاتر، کیفیت مسیر تحت تأثیر تعداد سطوح سلسله مراتبی تعریف شده در بالای سطح پایه قرار نمی گیرد. شایان ذکر است که ساختار چهاردرختی مورد استفاده در اینجا به هیچ وجه تنها گزینه قابل تصور برای ساخت سلسله مراتب سلسله مراتبی نیست. ساختار چهار درختی از آنجایی انتخاب شد که در ادبیات به خوبی شناخته شده است و پیاده سازی و مدیریت آن آسان است.
علاوه بر اندازه بلوک پایه و تعداد سطوح، کاربر همچنین می‌تواند هر تعداد انتقال را برای یک ورودی با تعیین حداکثر تعداد سلول‌هایی که می‌تواند توسط یک انتقال نشان داده شود، تعیین کند. برای هر ورودی، عرض ورودی بر این مقدار تقسیم می شود و از سقف ضریب برای تقسیم ورودی به قطعات با عرض مساوی استفاده می شود. سپس یک انتقال به طور جداگانه برای هر بخش، با توجه به استراتژی قرار دادن انتقال انتخاب شده، قرار می گیرد.

4.3. جستجوی نمودار

مشابه یافتن یک مسیر از طریق یک شبکه بزرگ جاده‌ای، معقول‌ترین راه برای یافتن مسیر با روش HPA* استفاده از بالاترین سطح سلسله مراتب تا حداکثر میزان ممکن است. این به روش اجازه می‌دهد تا بیشتر گره‌ها و لبه‌ها را در سطوح پایین‌تر کنار بگذارد و محاسبه را سریع‌تر تکمیل کند. بر اساس این اصل، روش مسیریابی به شرح زیر اجرا شده است.
الگوریتم یک گراف موقت Gt را می سازد که فقط شامل آن بخش هایی از سلسله مراتب اصلی نمودارها است که برای یافتن مسیری بین دو مکان داده شده s و d ضروری است. اولاً، بالاترین سطح سلسله مراتب به عنوان مبنای G t عمل می کند (در اینجا بالاترین سطح L l به طور کامل در نمودار موقت گنجانده شده است، اما در مورد مناطق و نمودارهای بسیار بزرگ، میزان انتزاع بالاترین سطح تا چه حد است. که در G t گنجانده شده است باید بر اساس برخی معیارها مشخص شود). دوم، بلوک حاوی s در سطح L l (ب o ) مشخص می شود. زیرگراف های مرتبط با چهار بلوک از سطح L l -1 که در B o موجود هستند به Gt اضافه می شوند . این فرآیند به طور متوالی به سمت پایین در سراسر سلسله مراتب ادامه می یابد تا به سطح پایه ( L 1 ) برسد. در سطح پایه، s با محاسبه مسیرهای کم‌هزینه با استفاده از الگوریتم Dijkstra از طریق رستر هزینه اصلی به گره‌های مرزی بلوک سطح پایه حاوی s به Gt متصل می‌شود . البته همین روش برای d انجام می شودهمچنین. این به طور موثر به این معنی است که تنها دو جستجوی کوچک در رستر هزینه اصلی برای اتصال s و d به سطح پایه L l مورد نیاز است ، و از آن سطح، آنها به سطوح بالاتر سلسله مراتب متصل می شوند.
هنگامی که ساختار نمودار G t کامل شد، محاسبه یک مسیر بین s و d یک موضوع ساده برای اجرای الگوریتم A* بر روی Gt است. در این پیاده سازی، تابع فاصله تخمینی که برای هدایت جستجوی A* در جهت کلی گره مقصد استفاده می شود، بر اساس حاصل ضرب فاصله اقلیدسی بین n و d و کمترین مقدار هزینه واحد cmin است.موجود در شطرنجی هزینه جستجوی نمودار می تواند هم به صورت یک طرفه و هم به صورت دو طرفه انجام شود. با این حال، از آنجایی که آزمایش‌های اولیه نشان داد که با استفاده از تکنیک جستجوی دوطرفه هیچ پیشرفتی حاصل نشد، تنها جستجوی یک‌جهت در اجرای نهایی گنجانده شد. الگوریتم با یک صف اولویت با استفاده از یک پشته باینری پیاده سازی شد.

5. مورد آزمایشی

آزمایش روش اجرا شده با یک تصویر لندست موزاییک شده انجام شد که با طبقه‌بندی حداکثر احتمال طبقه‌بندی شده و مقادیر هزینه اختصاص داده شده از [ 3 ] گرفته شده است. سه شطرنجی کوچک‌تر به‌طور دلخواه از منطقه‌ای بین 25.5-27.3 درجه شرقی و 63.9-65.7 درجه شمالی (در مرکز فنلاند) انتخاب شدند. هر یک از این سه شطرنجی از 500 × 500 سلول با وضوح 30 متر تشکیل شده است، بنابراین مساحت 225 کیلومتر مربع را پوشش می دهد .. بیست و پنج نقطه برای هر شطرنجی انتخاب شد تا مکان هایی را نشان دهد که مسیرها بین آنها محاسبه می شد. انتخاب این نقاط کاملاً تصادفی نبود: ابتدا فقط مراکز سلول ها به عنوان نقاط بالقوه در نظر گرفته شدند. ثانیاً، حداقل فاصله 2000 متر بین هر دو نقطه مورد نیاز بود. این کار برای اطمینان از اینکه هر بلوک حاوی بیش از یک نقطه نیست، انجام شد تا امکان آزمایش مناسب قرارگیری انتقال را فراهم کند. برای هر یک از سه شطرنجی، مسیرهای بین هر جفت نقطه محاسبه شد. از آنجایی که هزینه پیمایش همسانگرد فرض می شود، محاسبه مسیرها فقط در یک جهت کافی بود. از این رو، تعداد مسیرها در هر رستر هزینه است

Ijgi 02 00996 i006

که در آن m تعداد مکان ها است. با بیست و پنج مکان، تعداد مسیرها 300 است. مسیرها ابتدا با روش معمولی و غیر سلسله مراتبی محاسبه شدند و مسیرهای بهینه واقعی را از نظر ساختار شطرنجی ارائه کردند. اینها به عنوان معیاری عمل می کنند که مسیرهای به دست آمده با روش HPA* را می توان با آن مقایسه کرد.

هدف از این مورد آزمایشی نمایش نتایج برای سه استراتژی مختلف قرار دادن انتقال از روش HPA* همراه با شش اندازه بلوک پایه مختلف (10 × 10، 20 × 20، 30 × 30، 40 × 40، 50 × 50 و 60 است. × 60 سلول)، و کیفیت مسیر را ارزیابی کنید (به عنوان تفاوت در مقایسه با مسیرهای محاسبه شده با استفاده از رویکرد سنتی و غیر سلسله مراتبی اندازه گیری می شود). اگرچه استفاده از تعداد بیشتری از انتقال ها می تواند کیفیت مسیر را بهبود بخشد، در این مطالعه روش تنها با هدف به حداقل رساندن اندازه نمودار، که به منزله نمایش ورودی با یک انتقال واحد است، آزمایش شد. علاوه بر کیفیت مسیر، هزینه محاسباتی نیز از نظر تعداد گره‌های پردازش شده در مرحله مسیریابی واقعی و گره‌های پردازش شده هنگام اتصال مکان‌ها و مکان‌ها ارزیابی شد .d به G t . در نهایت، تأثیر افزایش تعداد سطوح انتزاع بر تلاش محاسباتی مورد بررسی قرار گرفت.

6. نتایج

6.1. کیفیت مسیر

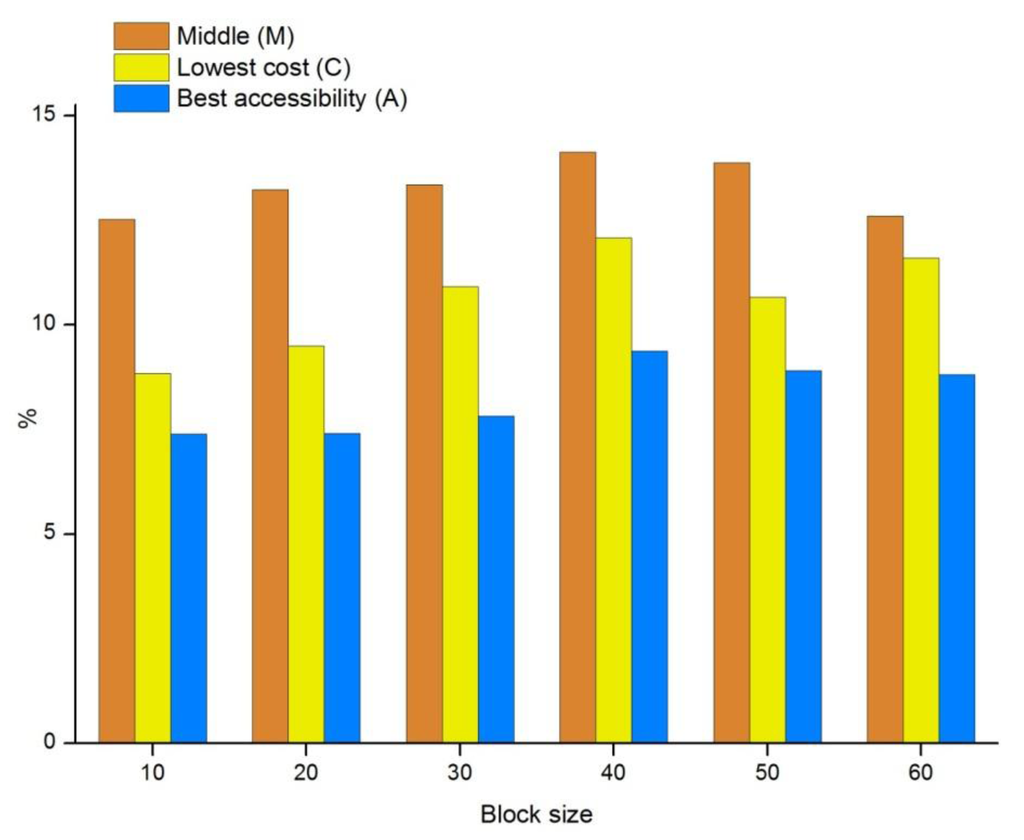
کیفیت مسیرهای محاسبه شده بر روی رسترهای آزمایشی با استفاده از روش HPA* با سه گزینه قرارگیری انتقال مختلف و شش اندازه بلوک مختلف در شکل 3 خلاصه شده است . کیفیت مسیر مرتبط با هر ترکیب به عنوان خطا در مقایسه با مسیرهای بهینه واقعی محاسبه شده با روش سنتی و غیر سلسله مراتبی بیان می شود. به عبارت دیگر، هرچه نوار کوتاهتر باشد، اختلاف کمتر است و روش مورد نظر را می توان عملکرد بهتری در نظر گرفت.
Ijgi 02 00996 g003 1024
شکل 3. خطا در مسیرهای محاسبه شده با روش HPA* با استفاده از سه گزینه قرارگیری انتقال مختلف و شش اندازه بلوک مختلف، در مقایسه با مسیرهای بهینه واقعی محاسبه شده با روش غیر سلسله مراتبی مرسوم.
خطای نشان داده شده در شکل 3 از حدود 7٪ تا 14٪، بسته به روش قرار دادن انتقال، و تا حدی کمتر، به اندازه بلوک انتخابی متغیر است. همانطور که انتظار می رود، خطا با گزینه قرار دادن انتقال M (وسط) بیشترین است. هر دو گزینه C (کمترین هزینه) و A (بهترین دسترسی) نتایج بهتری ارائه می دهند. روش A می تواند تا 20 درصد کاهش خطا در مقایسه با C و 50 درصد کاهش در مقایسه با M ارائه دهد. برای قرار دادن انحرافات مشاهده شده در یک چشم انداز مرتبط، می توان آنها را با حداکثر خطای کشیدگی 8.24 درصد مقایسه کرد [ 15 ].] ذاتاً با الگوی همسایگی هشت متصل مرسوم مرتبط است. همانطور که به نظر می رسد، A تنها تکنیک قرار دادن انتقال با خطای پیوسته کوچکتر از این است. البته، خطای متحمل شده توسط روش HPA* به خطای ازدیاد طول در مسیرهای مبتنی بر شطرنجی اضافه می‌شود، اما توجه به این نکته مهم است که خطای اضافه شده در استراتژی A در واقع کمتر از خطای ازدیاد طول است که معمولاً به عنوان خطا در نظر گرفته می‌شود. قابل قبول
تأثیر اندازه بلوک بر کیفیت مسیر به استراتژی قرار دادن انتقال انتخاب شده بستگی دارد. همانطور که نتایج نشان می‌دهد، به نظر می‌رسد که M و A نسبت به C نسبت به اندازه بلوک حساسیت کمتری دارند. این ممکن است به احتمال زیاد انتقال‌های بد موقعیت زمانی که استراتژی C استفاده می‌شود، نسبت داده شود، که با اندازه بلوک‌های بزرگ و ورودی‌های گسترده تقویت می‌شود. این یک جنبه مهم است، زیرا اندازه بلوک یک عامل کلیدی برای تعیین هزینه محاسباتی روش است.

6.2. عملکرد محاسباتی

دو جنبه در مورد روش مورد بررسی وجود دارد: پیش پردازش و مرحله مسیریابی واقعی. در حالی که دومی بدیهی است که حیاتی تر است، عملکرد اولی نیز در برنامه های کاربردی دنیای واقعی مهم است.
البته لازم به تاکید است که در این مطالعه روش HPA* برای مقاصد تجربی اجرا شده است تا امکان مقایسه بین روش‌ها به جای دستیابی به عملکرد بالا به صورت مطلق را فراهم کند. به عنوان مثال، محاسبه یک مسیر مستقیماً بر روی یکی از رسترهای آزمایشی بدون ایجاد یک انتزاع سلسله مراتبی در ابتدا ممکن است با روش اجرا شده تا نیم ساعت طول بکشد. این زمان بسیار طولانی است با توجه به اینکه انجام دقیقاً همان محاسبه با استفاده از توابع سطح هزینه داخلی نرم افزار پیشرفته GIS، مانند ArcGIS، تنها چند ثانیه طول می کشد. از این منظر،
پیش پردازش هر یک از رسترهای آزمایشی مورد استفاده در این مطالعه حدود ده دقیقه با استفاده از یک رایانه رومیزی با پردازنده 3.30 گیگاهرتز و 8 گیگابایت حافظه طول می کشد. این در مورد استراتژی‌های M و C صدق می‌کند، که زمان پیش‌پردازش، در اصل، مستقل از اندازه بلوک پایه انتخاب شده است. در مقابل، با استراتژی A، زمان مربوطه چندین ساعت است و با اندازه بلوک افزایش می یابد. با معرفی سطوح سلسله مراتبی بیشتر، زمان پیش پردازش برای همه گزینه های استراتژی اندکی افزایش می یابد و زمان محاسبه مسیر به ترتیب کوتاه تر می شود.
با توجه به این واقعیت که تلاش محاسباتی مورد نیاز برای محاسبه مسیرها همیشه به ویژگی‌های پیاده‌سازی نرم‌افزار و سخت‌افزار مورد استفاده برای انجام محاسبات وابسته است، ارزیابی زمان‌های پردازش مطلق برای ارزیابی عملکرد چندان مفید نیست. در عوض، یک راه بهتر ارزیابی تعداد گره‌های پردازش شده با روش‌های مختلف است، زیرا تلاش محاسباتی مسیریابی کم و بیش مستقیماً به تعداد گره‌هایی که باید در طول جستجوی نمودار بازدید شوند، بستگی دارد.
از نظر تعداد گره های پردازش شده، روش HPA* می تواند تا بیش از 95 درصد کاهش را در مقایسه با رویکرد سنتی و غیر سلسله مراتبی ارائه دهد ( شکل 4 ). در حالی که این کاهش را می توان بدون توجه به استراتژی قرار دادن انتقال به دست آورد، میزان دقیق بهبود بالقوه به اندازه بلوک بستگی دارد. از سوی دیگر، به دلیل ماهیت تابع پیچیدگی جستجوی نمودار، کاهش حاصل در زمان محاسبات ممکن است حتی بیشتر از چیزی باشد که با کاهش تعداد گره ها نشان داده می شود.
شکل 4 همچنین نشان می دهد که چگونه تعداد کل گره های پردازش شده بین گره های پردازش شده در اتصال s و d به نمودار و گره هایی که در انجام محاسبه مسیر واقعی پردازش می شوند، تقسیم می شود. بدیهی است که هزینه محاسباتی اتصال s و dبه نمودار با اندازه بلوک های کوچک کم است زیرا تعداد سلول های موجود در یک بلوک کوچک است. با این حال، با افزایش اندازه بلوک، هزینه محاسباتی به سرعت رشد می کند. دقیقا برعکس برای هزینه محاسباتی مرحله مسیریابی صادق است. با اندازه بلوک کوچک، نمودار از تعداد گره ها و لبه های بیشتری نسبت به اندازه بلوک های بزرگتر تشکیل شده است. هنگامی که روش HPA* فقط با یک سطح بلوک استفاده می شود، اندازه بلوک بهینه از نظر هزینه محاسباتی، اندازه ای است که تعداد کلی گره های پردازش شده را به حداقل می رساند.
Ijgi 02 00996 g004 1024
شکل 4. تعداد کل گره های پردازش شده در روش HPA* با شش اندازه بلوک مختلف. میله ها درصد گره های پردازش شده را در مقایسه با روش سنتی و غیر سلسله مراتبی، به طور جداگانه برای گره های پردازش شده در فرآیند مسیریابی واقعی و گره های پردازش شده برای اتصال موقت s و d به نمودار نشان می دهند.
هزینه محاسباتی اتصال s و d به نمودار تقریباً به طور کامل به اندازه بلوک وابسته است و بنابراین بسیار قابل پیش بینی است. با این حال، هزینه محاسباتی مرحله واقعی مسیریابی بیشتر به داده ها بستگی دارد، که چگالی انتقال در امتداد مرزهای بلوک را تعیین می کند. اگر یک رستر به بلوک‌های c × r تقسیم شود ، حداقل تعداد انتقال‌ها خواهد بود

Ijgi 02 00996 i007

از آنجایی که هر انتقال از دو گره تشکیل شده است، تعداد گره ها در آن زمان است

Ijgi 02 00996 i008

این زمانی درست است که هر مرز بین بلوک‌های مجاور فقط یک ورودی را در بر می‌گیرد، که همیشه برای شطرنج‌های بدون مانع صادق است. از طرف دیگر، تعداد انتقال‌ها و گره‌ها زمانی به حداکثر می‌رسد که سلول‌های مانع هر مرز را به حداکثر تعداد ممکن ورودی جداگانه تقسیم می‌کنند. در چنین حالتی تعداد گره ها می باشد

Ijgi 02 00996 i009

که در آن w عرض بلوک در سلول ها است.

6.3. سلسله مراتب چند سطحی

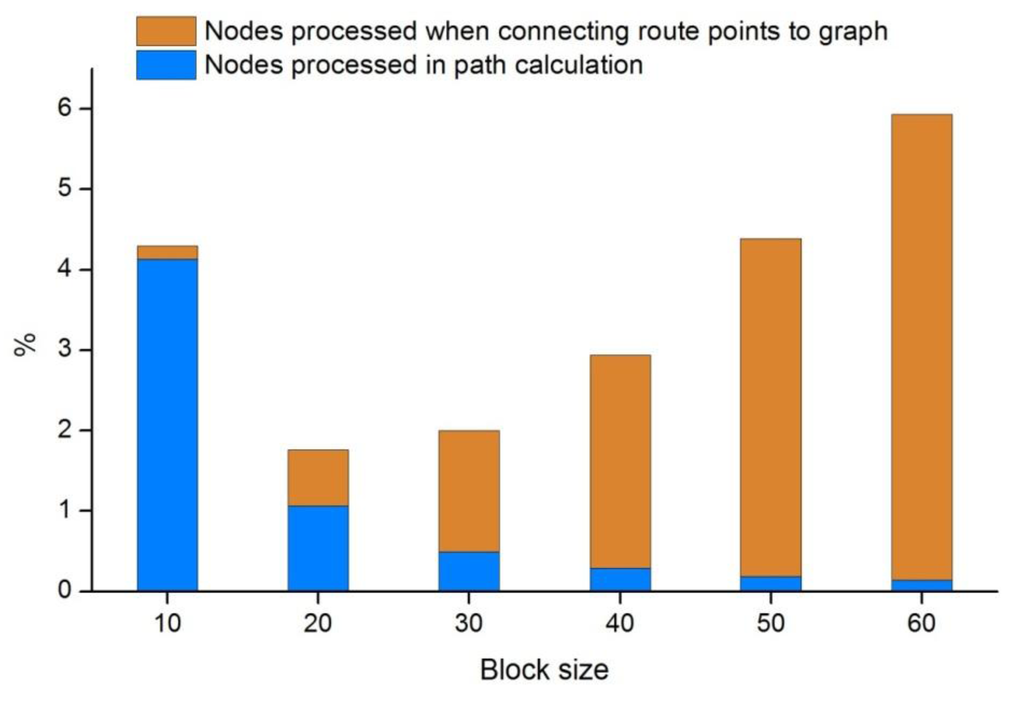
به جای تلاش برای تعیین اندازه یک بلوک بهینه، استفاده از توانایی HPA* برای کار با چندین سطح از انتزاع مفیدتر است. استفاده از اندازه بلوک پایه کوچک باعث می شود s و d به سرعت به نمودار متصل شوند، در حالی که انتزاعات سطح بالاتر برای یافتن سریع یک مسیر بین آنها استفاده می شود. شکل 5 نشان می دهد که چگونه تعداد گره های پردازش شده به تعداد سطوح سلسله مراتبی استفاده شده وابسته است. با داده های مورد استفاده در این مطالعه و اندازه بلوک پایه 10 × 10 سلول، تعداد گره های پردازش شده اندکی بیش از چهار درصد از روش غیر سلسله مراتبی سنتی است. به بیان دیگر، HPA* باعث کاهش بیش از 95 درصدی تعداد گره های پردازش شده می شود.
Ijgi 02 00996 g005 1024
شکل 5. درصد گره های پردازش شده در جستجوی گراف که با استفاده از روش HPA* با تعداد سطوح سلسله مراتبی متفاوت در مقایسه با روش سنتی و غیر سلسله مراتبی انجام شده است. اندازه بلوک پایه 10 × 10 سلول است.
هنگامی که سطوح بیشتری از انتزاع معرفی می شوند، تعداد گره های پردازش شده بیشتر کاهش می یابد. با یک سلسله مراتب سه سطحی، تعداد گره های پردازش شده به یک چهارم سطح پایه 10 سلولی کاهش می یابد. از آنجایی که کیفیت مسیر بدون توجه به تعداد سطوح سلسله مراتبی دست نخورده باقی می ماند، تنها ایراد استفاده از سلسله مراتب بیشتر، هزینه های سربار ناشی از مدیریت چندین سطح است که در درجه اول بر مرحله پیش پردازش تأثیر می گذارد.

7. بحث

در حالی که روش HPA* می تواند یک مزیت محاسباتی قابل توجهی برای مسیریابی در شطرنجی های با هزینه بالا ارائه دهد، همچنین دارای معایب خاصی است که باید در نظر گرفته شود. انتقاد اصلی روش، انحراف مسیرها از بهینه واقعی است که نتیجه اجتناب ناپذیر انتزاع است. حتی زمانی که این خطا خیلی زیاد نباشد، به خطای ذاتی موجود در مسیرهای مبتنی بر شطرنجی اضافه می کند. خطا را می توان با اجازه دادن به انتقال بیشتر در هر ورودی کاهش داد و در نتیجه نمایش دقیق تری از گزینه های حرکت به دست آورد. باز هم، این به قیمت افزایش هزینه محاسباتی در مرحله مسیریابی است، که ممکن است در برنامه هایی که نیاز به پاسخ فوری دارند، بازدارنده باشد.
یک منبع دیگر از خطا ناشی از این واقعیت است که انتقال‌ها فقط اجازه می‌دهند از مرزهای بلوک به صورت متعامد عبور کنند. با این حال، این فقط یک موضوع پیاده سازی است، زیرا انتقال های مورب می تواند مورد توجه قرار گیرد، برای مثال، با استفاده از یک الگوی قرار دادن گره که در آن گره ها در مرزهای سلولی به جای مراکز سلول قرار می گیرند [ 16 ، 20 ]. با استفاده از این رویه، یک انتقال تنها شامل یک گره می‌شود که در مرز بین دو بلوک قرار دارد، که انعطاف‌پذیری بیشتری را در مورد جهت‌هایی که از آن مرز می‌توان عبور کرد، ارائه می‌دهد. این همچنین مزیت محاسباتی را با کاهش تعداد گره ها در انتزاع فراهم می کند. با این حال، وزنه تعادل این گزینه یک مرحله پیش پردازش پیچیده تر خواهد بود.
برخی از جنبه های اضافی در مورد روش توصیف شده، یا اجرای آن وجود دارد که می تواند متفاوت انجام شود. در این مورد و همچنین در اجرای نویسندگان اصلی روش HPA*، انتزاعات سطح بالاتر بر روی انتزاع سطح پایه ساخته می شوند. این دو مزیت مهم دارد. اولاً، ساختن انتزاعات سطح بالاتر را می توان به سرعت انجام داد، و ثانیاً، نتایج بدون توجه به تعداد سطوح سلسله مراتبی استفاده شده همیشه یکسان باقی می مانند. با این حال، می توان انتقال ها (و درون یال ها) را به طور مستقل برای هر سطح از انتزاع تعریف کرد. این انعطاف پذیری بیشتری را در قرار دادن انتقال ها فراهم می کند، که به نوبه خود می تواند کیفیت مسیر را، به ویژه در سطوح بسیار بالای انتزاع، بهبود بخشد. در حقیقت، این روش در مرحله اولیه مطالعه با نتایج نسبتا امیدوارکننده آزمایش شد، اما متعاقباً به دلیل زمان غیرعملی طولانی پیش پردازش کنار گذاشته شد. یک موضوع دیگر، سازگاری نتایج است، زیرا نتایج همیشه به تعداد سطوح انتزاعی مورد استفاده بستگی دارد.
یکی دیگر از اصلاحات روش ممکن است حفظ تنها یک انتقال واحد در هر ورودی در همه سطوح باشد. در روش پیاده سازی شده، تمام انتقال های تعریف شده در سطح پایه تا زمانی که با مرزهای بلوک های سطح بالاتر مطابقت داشته باشند، به سطوح بالاتر منتقل می شوند. با این حال، این بیش از آن چیزی است که برای اطمینان از اتصال در سطوح بالاتر لازم است. با تعریف مجدد ورودی ها در هر سطح، و انتخاب تنها یک انتقال واحد از سطح پایین برای نشان دادن ورودی در سطح بالاتر، اندازه نمودار می تواند به طور قابل توجهی کاهش یابد. آزمایشی با این روش نیز انجام شد. تلاش محاسباتی در واقع کاهش یافت، اما به عنوان یک اثر منفی، خطا به سطح غیرقابل قبولی بالای 15٪ تا 40٪ افزایش یافت. مسیری که به این روش محاسبه می‌شود، می‌تواند در مرحله پس پردازش با محاسبه مجدد مسیر در انتزاعات سطح پایین‌تر با استفاده از بلوک‌های سطح بالاتر متقاطع شده به عنوان «ماسک» که جستجو را در سطح پایین‌تر مشخص می‌کند، اصلاح شود. در حالی که مسیر را می توان به این روش اصلاح کرد، هزینه محاسباتی متحمل شده توسط مرحله پس پردازش، هر گونه مزیتی را که با جداسازی نمودار به دست می آید، لغو می کند.

8. نتیجه گیری

هدف از این مطالعه نشان دادن و ارزیابی روش HPA * برای مسیریابی بر روی رسترهای هزینه با هزینه غیر یکنواخت، و پیشنهاد یک بهبود به منظور تقریب بهتر مسیرهای بهینه در رسترهای این نوع بود. ابزار آزمایشی در GIS پیاده‌سازی شد و با داده‌های مبتنی بر تصاویر ماهواره‌ای مورد آزمایش قرار گرفت. یک هدف خاص آزمایش این بود که آیا یک استراتژی قرار دادن انتقال مبتنی بر مفهوم دسترسی، می‌تواند مسیرهای بهتری نسبت به تکنیک‌های ابتدایی‌تر ایجاد کند یا خیر.
نتایج نشان داد که روش قرار دادن انتقال بر اساس امتیاز دسترسی ممکن است در واقع یک تکنیک ارجح در مقایسه با قرار دادن انتقال در وسط ورودی یا موقعیت با کمترین هزینه پیمایش باشد. نتایج با این فرضیه اصلی مطابقت دارند که قرار دادن انتقال بر اساس دسترسی، کیفیت مسیر را بهبود می‌بخشد، به خصوص زمانی که تعداد انتقال‌ها به حداقل برسد. در واقع مزیت این استراتژی دو چندان است. اول، با توجه به نتایج، به طور یکنواخت نتایج بهتری نسبت به سایر جایگزین های آزمایش شده ارائه می دهد. دوم، آن را نیز فراهم می کند سازگار استنتایج، حساسیت کمتری نسبت به انتخاب اندازه بلوک است. نقطه ضعف استراتژی مبتنی بر دسترسی پیشنهادی در مقایسه با سایر تکنیک‌ها، مرحله پیش پردازش گسترده است که ممکن است این تکنیک را غیرعملی کند. با این وجود، پیش پردازش باید فقط یک بار انجام شود تا زمانی که رستر هزینه اصلی بدون تغییر باقی بماند، و حتی اگر تغییراتی رخ دهد، پیش پردازش باید فقط برای بلوک های تحت تأثیر تغییرات انجام شود. همچنین می توان نحوه محاسبه امتیاز دسترسی را اصلاح کرد و در نتیجه تعداد مسیرهای در نظر گرفته شده را محدود کرد، بنابراین هزینه محاسباتی را کاهش داد اما کیفیت نتایج را تا حدی کاهش داد.
به طور کلی، روش HPA* برای کاربردهای GIS مناسب است که در آن مسیریابی خارج از شبکه باید با منابع محاسباتی کوچک و در مدت زمان محدود انجام شود، یا زمانی که مسیرها باید به طور مکرر در یک منطقه خاص محاسبه شوند، مانند در حالت خاموش. برنامه های ناوبری جاده و برنامه ریزی مسیر. اگرچه این روش در جاهای دیگر مورد مطالعه قرار گرفته است، قابل توجه است که بیشتر تحقیقات در مورد این موضوع در زمینه هایی غیر از جغرافیا، مانند رباتیک و بازی های رایانه ای انجام می شود و روش های توسعه یافته در این زمینه ها ممکن است همیشه به طور ایده آل مناسب نباشند. بافت جغرافیایی این مطالعه تلاشی را برای آوردن بخشی از دانش موجود در سایر زمینه‌ها به حوزه جغرافیا و GIS و گسترش آن برای تطابق بیشتر با اهداف متنوع نشان می‌دهد.

منابع

  1. Balstrøm, T. در شناسایی مسیر پیاده‌روی با بیشترین صرفه‌جویی در زمان در یک زمین کوهستانی بدون مسیر. Geogr. Tidsskr. 2002 ، 102 ، 51-58. [ Google Scholar ]
  2. ریس، WG مسیرهای کم‌هزینه در زمین‌های کوهستانی. محاسبه کنید. Geosci. 2004 ، 30 ، 203-209. [ Google Scholar ] [ CrossRef ]
  3. استور، ر. Antikainen، H. استفاده از ارزیابی چند معیاره مبتنی بر GIS و بهینه سازی مسیر برای موجودی موثر میدان جنگل. محاسبه کنید. محیط زیست شهری 2010 ، 34 ، 153-161. [ Google Scholar ] [ CrossRef ]
  4. فلدمن، SC; Pelletier, RE; والسر، ای. اسموت، جی سی. Ahl, D. نمونه اولیه برای مسیریابی خط لوله با استفاده از داده های سنجش از دور و تجزیه و تحلیل سیستم اطلاعات جغرافیایی. سنسور از راه دور محیط. 1995 ، 53 ، 123-131. [ Google Scholar ] [ CrossRef ]
  5. Xiang، W.-N. یک روش مبتنی بر GIS برای برنامه ریزی تراز مسیر. Landsc. طرح شهری. 1996 ، 35 ، 11-23. [ Google Scholar ] [ CrossRef ]
  6. کولیشون، دبلیو. Pilar, JV یک الگوریتم مسیر کمترین هزینه وابسته به جهت برای جاده ها و کانال ها. بین المللی جی. جئوگر. Inf. علمی 2000 ، 14 ، 397-406. [ Google Scholar ] [ CrossRef ]
  7. یو، سی. لی، جی. Munro-Stasiuk، MJ توسعه‌های الگوریتم‌های مسیر کم‌هزینه برای برنامه‌ریزی راه. بین المللی جی. جئوگر. Inf. علمی 2003 ، 17 ، 361-376. [ Google Scholar ] [ CrossRef ]
  8. باگلی، س. ژنلتی، دی. Orsi، F. مسیریابی خطوط برق از طریق تحلیل مسیر کم هزینه و ارزیابی چند معیاره برای به حداقل رساندن اثرات زیست محیطی. محیط زیست ارزیابی های تاثیر 2011 ، 31 ، 234-239. [ Google Scholar ] [ CrossRef ]
  9. Diestel, R. Graph Theory , 2nd ed.; Springer-Verlag: نیویورک، نیویورک، ایالات متحده آمریکا، 2000; پ. 2. [ Google Scholar ]
  10. میلر، اچ جی; شاو، اس.-ال. مدل های داده GIS-T. در سیستم های اطلاعات جغرافیایی برای حمل و نقل ; انتشارات دانشگاه آکسفورد: نیویورک، نیویورک، ایالات متحده آمریکا، 2001; صص 54-55. [ Google Scholar ]
  11. داگلاس، مسیر کمترین هزینه DH در GIS با استفاده از سطح هزینه انباشته و خطوط شیبدار. کارتوگر. بین المللی جی. جئوگر. Inf. جئوویس. 1994 ، 31 ، 37-51. [ Google Scholar ]
  12. Goodchild، سیستم های اطلاعات جغرافیایی MF و مدل سازی حمل و نقل تفکیک شده. Geogr. سیستم 1998 ، 5 ، 19-44. [ Google Scholar ]
  13. دی اسمیت، ام جی; Goodchild، MF; Longley, PA Geospatial Analysis , 2nd ed.; Winchelsea Press: لستر، انگلستان، 2007; صص 149-152. [ Google Scholar ]
  14. خو، جی. Lathrop, RG, Jr. بهبود دقت شبیه‌سازی پدیده‌های گسترش در یک سیستم اطلاعات جغرافیایی مبتنی بر شطرنجی. بین المللی جی. جئوگر. Inf. سیستم 1995 ، 9 ، 153-168. [ Google Scholar ] [ CrossRef ]
  15. Goodchild، MF ارزیابی راه حل های شبکه برای مشکل مکان راهرو. محیط زیست طرح. A 1977 , 9 , 727-738. [ Google Scholar ]
  16. ون بملن، جی. کواک، دبلیو. ون هکن، م. van Oosterom، P. Vector vs. الگوریتم‌های مبتنی بر شطرنجی برای برنامه‌ریزی حرکت متقابل کشوری. در مجموعه مقالات یازدهمین سمپوزیوم بین المللی کارتوگرافی به کمک کامپیوتر، مینیاپولیس، MN، ایالات متحده، 31 اکتبر تا 1 نوامبر 1993. صص 304-317.
  17. بولستاد، بی. تحلیل های رستر. در مبانی GIS ; Eider Press: دریاچه خرس سفید، MN، ایالات متحده آمریکا، 2002; ص 283-285. [ Google Scholar ]
  18. Dijkstra، EW یادداشتی در مورد دو مشکل در ارتباط با نمودارها. عدد. ریاضی. 1959 ، 1 ، 269-271. [ Google Scholar ] [ CrossRef ]
  19. کورمن، تی. Leiserson، CE; Rivest، RL کوتاهترین مسیرهای تک منبعی. در مقدمه ای بر الگوریتم ها ; مطبوعات MIT: کمبریج، MA، ایالات متحده آمریکا، 1990; صص 527-532. [ Google Scholar ]
  20. Antikainen, H. مقایسه استراتژی‌های مختلف برای تعیین مسیرهای کم‌هزینه مبتنی بر شطرنجی با حداقل مقدار اعوجاج. ترانس. GIS 2013 ، 17 ، 96-108. [ Google Scholar ] [ CrossRef ]
  21. Tomlin, D. انتشار امواج شعاعی هزینه سفر در یک شبکه. بین المللی جی. جئوگر. Inf. علمی 2010 ، 24 ، 1391-1413. [ Google Scholar ] [ CrossRef ]
  22. فو، ال. سان، دی. الگوریتم‌های کوتاه‌ترین مسیر اکتشافی Rilett، RL برای کاربردهای حمل‌ونقل: وضعیت هنر. محاسبه کنید. اپراتور Res. 2006 ، 33 ، 3324-3343. [ Google Scholar ] [ CrossRef ]
  23. هارت، PE; نیلسون، نیوجرسی؛ رافائل، بی. مبنایی رسمی برای تعیین اکتشافی مسیرهای حداقل هزینه. IEEE Trans. سیستم علمی سایبرن. 1968 ، 4 ، 100-107. [ Google Scholar ] [ CrossRef ]
  24. راسل، اس. Norvig, P. Informed Search and Exploration. در هوش مصنوعی ، ویرایش دوم. Prentice Hall: Upper Saddle River, NJ, USA, 2003; صص 97-101. [ Google Scholar ]
  25. پرل، جی. خصوصیات صوری روشهای اکتشافی. در اکتشافی ؛ Addison-Wesley: Reading، MA، ایالات متحده آمریکا، 1984; صص 77-78. [ Google Scholar ]
  26. سلطانی، ع. توفیق، ح. گولرماس، جی. فرناندو، T. برنامه ریزی مسیر در سایت های ساخت و ساز: ارزیابی عملکرد الگوریتم های جستجوی Dijkstra، A * و GA. Adv. مهندس به اطلاع رساندن. 2002 ، 16 ، 291-303. [ Google Scholar ]
  27. دوریگو، م. استوتزل، تی. فراابتکاری بهینه سازی کلونی مورچه ها: الگوریتم ها، کاربردها و پیشرفت ها. در راهنمای فراابتکاری ; گلاور، اف.، کوچنبرگر، GA، ویرایش. Kluwer Academic Publishers: Secaucus, NJ, USA, 2002; صص 251-285. [ Google Scholar ]
  28. ریشیوال، وی. یداو، م. Arya, KV یافتن مسیرهای بهینه در نقشه های زمین با استفاده از الگوریتم کلونی مورچه ها. بین المللی جی. کامپیوتر. مهندس تئوری 2010 ، 2 ، 1793-8201. [ Google Scholar ]
  29. جائن، جی. موچولی، JA; کاتالا، آ. مورچه ناوارو، ای. دیجیتالز به عنوان بهترین سیسرون برای بازدیدکنندگان موزه. Appl. محاسبات نرم. 2011 ، 11 ، 111-119. [ Google Scholar ] [ CrossRef ]
  30. گلدبرگ، DE مقدمه ای ملایم بر الگوریتم های ژنتیک. در الگوریتم های ژنتیک در جستجو، بهینه سازی و یادگیری ماشینی ؛ ادیسون-وسلی: بوستون، MA، ایالات متحده آمریکا، 1989; صص 1-2. [ Google Scholar ]
  31. Ahn، CW; راماکریشنا، RS یک الگوریتم ژنتیک برای مشکل مسیریابی کوتاه ترین مسیر و اندازه جمعیت. IEEE Trans. تکامل. محاسبه کنید. 2002 ، 6 ، 566-579. [ Google Scholar ]
  32. ژانگ، ایکس. آرمسترانگ، الگوریتم‌های ژنتیک MP و مسئله مکان‌یابی راهرو: اهداف چندگانه و راه‌حل‌های جایگزین محیط زیست طرح. B 2008 , 35 , 148-168. [ Google Scholar ]
  33. لی، جی. Yang, J. DGA: یک الگوریتم مسیریابی مجدد سریع و مقیاس پذیر بر اساس کوتاه ترین مسیر و الگوریتم های ژنتیک. بین المللی جی. کامپیوتر. اشتراک. 2012 ، 7 ، 482-493. [ Google Scholar ]
  34. Pohl, I. جستجوی دو جهته و اکتشافی در مسائل مسیر . گزارش فنی 104; مرکز شتاب دهنده خطی استانفورد: استانفورد، کالیفرنیا، ایالات متحده آمریکا، 1969. [ Google Scholar ]
  35. استراتژی‌های جستجوی Nilsson، NJ برای سیستم‌های تولید هوش مصنوعی. در اصول هوش مصنوعی ; Tioga Publishing: Palo Alto, CA, USA, 1980; صص 88-90. [ Google Scholar ]
  36. کایندل، اچ. Kainz، G. جستجوی اکتشافی دو جهته مورد بازنگری قرار گرفت. جی آرتیف. هوشمند Res. 1997 ، 7 ، 283-317. [ Google Scholar ]
  37. د شامپو، دی. Sint، L. یک الگوریتم جستجوی اکتشافی دو طرفه بهبود یافته. J. Assoc. محاسبه کنید. ماخ 1977 ، 24 ، 177-191. [ Google Scholar ]
  38. Kwa، JBH BS*: یک الگوریتم جستجوی اکتشافی مرحله‌ای دو جهته قابل قبول. آرتیف. هوشمند 1989 ، 38 ، 95-109. [ Google Scholar ]
  39. صامت، ح. مقدمه. در کاربردهای ساختار داده های مکانی ; Addison-Wesley: Reading، MA، USA، 1990; ص 2-3. [ Google Scholar ]
  40. کامبامپاتی، اس. دیویس، LS برنامه ریزی مسیر چند رزولوشن برای روبات های سیار. ربات IEEE J. خودکار 1986 ، 2 ، 135-145. [ Google Scholar ] [ CrossRef ]
  41. چن، DZ; Szczerba، RJ; Uhran, JJ, Jr. رویکرد چهاردرخت قاب‌دار برای تعیین کوتاه‌ترین مسیرهای اقلیدسی در یک محیط دو بعدی. IEEE Trans. ربات. خودکار 1997 ، 13 ، 668-681. [ Google Scholar ] [ CrossRef ]
  42. استورتوان، ن. Jansen, R. An Analysis of Map-based Abstraction and Refinement. در مجموعه مقالات هفتمین سمپوزیوم بین‌المللی در مورد انتزاع، فرمول‌بندی و تقریب، ویستلر، کانادا، 18 تا 21 ژوئیه 2007. صص 344-358.
  43. بوته آ، ا. مولر، ام. Schaeffer, J. مسیریابی سلسله مراتبی نزدیک به بهینه. J. Game Dev. 2004 ، 1 ، 7-28. [ Google Scholar ]
  44. جانسن، ام.آر. Buro، M. HPA* بهبود. در مجموعه مقالات سومین کنفرانس هوش مصنوعی و سرگرمی دیجیتال تعاملی استنفورد، استانفورد، کالیفرنیا، ایالات متحده آمریکا، 6 تا 8 ژوئن 2007. صص 84-87.
  45. هارابور، دی. Botea، A. برنامه ریزی مسیر سلسله مراتبی برای عوامل چند اندازه در محیط های ناهمگن. در مجموعه مقالات سمپوزیوم IEEE در مورد هوش محاسباتی و بازی ها، پرت، استرالیا، 15-18 دسامبر 2008. صص 258-265.
  46. لی، ی. سو، ال.-م. لی، مسیریابی سلسله مراتبی WL بر اساس درخت تصمیم. در مجموعه مقالات هفتمین کنفرانس بین المللی مجموعه های خشن و فناوری دانش، چنگدو، چین، 17 تا 20 اوت 2012. ص 248-256.

;کاربردهای GISمقالات

آموزش کاربردی ArcGISالهام ابراهیم زادهکاربرد جی ای اسکاربرد جی ای اس در زمین شناسی

بدون نظر

دیدگاهتان را بنویسید

نشانی ایمیل شما منتشر نخواهد شد. بخش‌های موردنیاز علامت‌گذاری شده‌اند *

همواره حمایت دانشجویان عزیزمان همراه ما بوده و این سببب شده که گامی محکم به‌سوی ایجاد یک مرجع برای آموزش GIS برداریم. با این امید که بتوانیم قدردان حمایت شما بزرگواران باشیم.

  • خانه
  • آموزش
  • فیلم آموزشی
  • تماس با ما
  • درباره ما
  • وبلاگ
  • سمنان /خیابان کاشانی/ساختمان فناوری اطلاعات/پ 8
  • 09120049370