تجزیه و تحلیل تغییرات فضایی پدیده های محدود شده توسط شبکه ارائه شده توسط یک ویژگی پیوند با استفاده از مدل بیزی سلسله مراتبی

خلاصه

تنوع مکانی پدیده های جغرافیایی یک مشکل کلاسیک در تجزیه و تحلیل داده های مکانی است و می تواند بینشی در مورد فرآیندهای اساسی ارائه دهد. روش‌های اکتشافی سنتی بیشتر به فرض فاصله مسطح بستگی دارند، اما بسیاری از پدیده‌های فضایی به زیر مجموعه‌ای از فضای اقلیدسی محدود می‌شوند. در این مطالعه، ما یک روش مبتنی بر یک مدل بیزی سلسله مراتبی را برای تجزیه و تحلیل تغییرات فضایی پدیده‌های محدود شبکه که با یک ویژگی پیوند در رابطه با دو آزمایش مبتنی بر یک شبکه فرضی ساده‌شده و یک شبکه جاده‌ای پیچیده در شنژن که شامل 4212 است، اعمال می‌کنیم. نقاط مورد علاقه تسهیلات شهری (POI) برای فعالیت های اوقات فراغت. سپس، روش‌هایی با نام شاخص‌های محلی خوشه‌های محدود به شبکه (LINCS) برای کشف الگوهای فضایی محلی در فضای شبکه داده شده اعمال می‌شوند. روش پیشنهادی برای پدیده‌هایی طراحی شده است که با مقادیر ویژگی پیوندهای شبکه نشان داده می‌شوند و قادر به حذف بخشی از تغییرات تصادفی ناشی از تخمین نمونه‌های کوچک هستند. اثرات وابستگی فضایی و توزیع پایه نیز در روش پیشنهادی در نظر گرفته شده است که می تواند در زمینه های برنامه ریزی شهری و تحقیقات ایمنی کاربرد داشته باشد.

کلید واژه ها:

شبکه محدود ; نقاط مورد علاقه ؛ مدل بیزی سلسله مراتبی ; روش مبتنی بر ویژگی ; شاخص‌های محلی خوشه‌های محدود به شبکه (LINCS)

1. معرفی

تنوع فضایی یک مشکل کلاسیک در تجزیه و تحلیل داده های مکانی است و می تواند بینشی در مورد الگوهای فضایی پدیده های جغرافیایی و فرآیندهای فضایی ارائه دهد. در روش‌های تحلیل سنتی، عموماً فرض می‌شود که رویدادهای فضایی را می‌توان به صورت تصادفی در یک صفحه قرار داد، و ارتباط فضایی بین مکان‌های رویداد یا مناطق فرعی با استفاده از فاصله اقلیدسی (یا مسطح) تحلیل می‌شود [1 ، 2 ، 3 ] ، که در آن فرآیندهای فضایی ذاتی بر اساس فرض هندسه اقلیدسی [ 4] کمی سازی می شوند.]. با این حال، زمانی که یک پدیده فضایی ظاهراً به زیرمجموعه ای از فضای جغرافیایی، مانند شبکه خیابان، محدود می شود، این فرض مناسب نیست. در دنیای واقعی، رویدادهای زیادی وجود دارد که وجود آنها توسط شبکه ها به شدت محدود شده است، مانند تصادفات وسایل نقلیه در جاده ها، خدمات خرده فروشی در کنار خیابان ها، جرایم خیابانی و بسیاری موارد دیگر. این رویدادها رویدادهای محدود شده شبکه یا رویدادهای شبکه به اختصار [ 4 ، 5 ، 6 ] نامیده می شوند. روش‌های مبتنی بر اقلیدسی، که برای رویدادهایی که در یک صفحه پیوسته روی می‌دهند، طراحی شده‌اند، احتمالاً هنگام تجزیه و تحلیل رویدادهای شبکه به نتایج مغرضانه منجر می‌شوند. بنابراین، تحلیل فضایی شبکه در دو دهه گذشته توسعه یافته است و به طور گسترده در تجزیه و تحلیل پدیده‌های فضایی محدود به شبکه استفاده می‌شود.7 ، 8 ، 9 ، 10 ، 11 ، 12 ، 13 ، 14 ، 15 ].

برای پدیده‌های فضایی متشکل از رویدادهای شبکه، بدیهی است که فرض فاصله اقلیدسی اغلب نقض می‌شود، زیرا شبکه و فضاهای اقلیدسی هم‌شکل نیستند و ویژگی‌های ذاتی خود را دارند [16 ] . به عنوان مثال، تصادفات وسایل نقلیه و تخلفات رانندگی در شبکه های جاده ای بیشتر از سایر مکان های داخل یک فضای مسطح رخ می دهد. علاوه بر این، فاصله اقلیدسی ممکن است معیار مناسبی برای جداسازی فضایی رویدادها [ 16 ] نباشد و برای تجزیه و تحلیل رویدادهای نقطه ای محدود شده در فضای شبکه نامناسب است [ 17] .]. رویدادهای نقطه نزدیک فضایی در فضای اقلیدسی می توانند در فضای شبکه هنگام محاسبه اتصال از یکدیگر دور باشند. به عنوان مثال، ایستگاه های اتوبوس بر اساس فاصله شبکه جاده ای از پیش تعریف شده به جای فاصله اقلیدسی طراحی شده اند. با این حال، در برخی شرایط، فرض فاصله اقلیدسی ممکن است برای تحلیل پدیده‌های محدود به شبکه مناسب باشد. به عنوان مثال، ارتباط بین قرار گرفتن در معرض آلودگی هوا مرتبط با ترافیک و مرگ و میر بیماری در سطح فردی با استفاده از بافر مبتنی بر فاصله اقلیدسی در اپیدمیولوژی تخمین زده می شود.

در تجزیه و تحلیل فضایی مسطح، داده های جغرافیایی ارجاع داده شده را می توان به عنوان رویدادهای نقطه ای (مثلاً تصادفات وسیله نقلیه، جنایات، یا مکان های مسکونی) یا به عنوان واحدهای فضایی با مقادیر ویژگی (مثلاً نرخ جمعیت یا بیماری) مشاهده کرد [18 ] . به طور مشابه، یک پدیده محدود به شبکه می تواند به عنوان مجموعه ای از نقاط توزیع شده بر روی پیوندهای شبکه یا به عنوان مجموعه ای از مقادیر مشخصه اختصاص داده شده به پیوندها نشان داده شود [ 5 ، 16 ]، که نیاز به روش های مختلف تجزیه و تحلیل را ایجاد می کند. این روش‌های آماری با استفاده از دو رویکرد رایج در تحلیل فضایی، یعنی رویکرد مبتنی بر ویژگی [ 5 ، 13 ، 16 ] و رویکرد مبتنی بر رویداد [ 5] توسعه یافته‌اند.، 6 ]. برای اولی، رویدادهای فضایی مستقیماً تجزیه و تحلیل نمی‌شوند، اما زمانی که مکان‌های دقیق رویدادهای مجزا مورد توجه یا در دسترس نباشند، به یک شبکه جاده اختصاص داده می‌شوند. تعداد تجمیع رویدادها به عنوان مقادیر ویژگی پیوندها در نظر گرفته می شود و این روش همچنین رویکرد مبتنی بر ویژگی پیوند نامیده می شود [ 16 ]. برای دومی، مکان های فیزیکی رویدادهای گسسته به طور مستقیم تجزیه و تحلیل می شوند. این مقاله یک روش مبتنی بر بیزی را برای تجزیه و تحلیل تغییرات فضایی پدیده‌های محدود به شبکه که با رویکرد ویژگی پیوند نشان داده می‌شوند، معرفی می‌کند. انگیزه این روش به شرح زیر است.

یک الگوی فضایی مشاهده شده از یک پدیده صرفاً می تواند ناشی از تغییرات فضایی توزیع پایه باشد و این امکان باید در تحلیل فضایی شبکه در نظر گرفته شود. به عنوان مثال، تنوع فضایی یک بیماری تا حد زیادی به توزیع جمعیت در معرض خطر بستگی دارد. بنابراین، روش استانداردسازی معمولاً برای محاسبه نسبتی مانند ریسک نسبی [ 19 ] بین شمارش رویدادهای مشاهده شده و شمارش رویدادهای مورد انتظار که با استفاده از توزیع پایه تعیین می شوند، اعمال می شود. علاوه بر این، پیوندها معمولاً به بخش‌های کوتاه‌تری به نام واحدهای فضایی پایه (BSUs) در رویکرد ویژگی پیوند تقسیم می‌شوند [ 13 ، 14 ، 15.]، که تشخیص الگوهای فضایی را با وضوح فضایی بسیار بهتر از آنچه توسط یک شبکه معین تحمیل شده است، امکان پذیر می سازد [ 16 ]. با این حال، تجزیه و تحلیل‌های مبتنی بر واحدهای فضایی ظریف با مقادیر پایه کوچک، یک منبع اضافی از تنوع را به دلیل تغییرات تصادفی وارد تحلیل می‌کنند [ 20 ]. به طور معمول، پیوندهایی با موارد کم (یا صفر) می‌توانند مقادیر شدید نسبت‌ها را ایجاد کنند، زیرا واریانس مقدار استاندارد شده با تعداد موارد مورد انتظار رابطه معکوس دارد و اندازه کوچک توزیع پایه باعث تغییرات زیادی در نتایج تخمین زده می‌شود. .

این مقاله روشی مبتنی بر مدل‌های بیزی سلسله مراتبی را برای تجزیه و تحلیل تغییرپذیری فضایی پدیده‌های محدود به شبکه با در نظر گرفتن تغییرات تصادفی ناشی از تخمین نمونه کوچک در ارتباط با دو آزمایش مبتنی بر یک شبکه فرضی ساده‌شده و یک شبکه جاده‌ای پیچیده در شنژن معرفی می‌کند. 4212 نقطه مورد علاقه تسهیلات شهری (POI) برای فعالیت های اوقات فراغت. برای شهرهای بزرگ چین که در حال رشد سریع اقتصادی و توسعه سریع شهری هستند، نیاز فوری به مطالعه ویژگی‌های توزیع فضایی امکانات شهری به منظور درک بهتر ساختار شهری و الگوهای تحرک انسانی وجود دارد. در یک محیط GIS (سیستم اطلاعات جغرافیایی)، POIهای تأسیسات شهری، درست مانند بسیاری از پدیده های جغرافیایی دیگر از جمله تصادفات اتومبیل در جاده، جنایات، و سایت های شیوع بیماری، می توانند به عنوان نقاطی برای تجزیه و تحلیل فضایی انتزاع شوند. نقاط می توانند واحدهای جغرافیایی خاص یا مکان رویدادهای گذشته باشند. بر اساس موقعیت مکانی این رویدادهای نقطه‌ای، تحلیل فضایی به طور گسترده برای مطالعه ویژگی‌های توزیع‌های فضایی جهانی یا محلی استفاده شده است.16 ]. ادامه این مقاله به شرح زیر سازماندهی شده است. مرور ادبیات در بخش 2 انجام شده است . بخش 3 چارچوب روش پیشنهادی و دو آزمایش را معرفی می کند. بخش 4 جزئیات برنامه و نتایج و مقایسه‌ها را با استفاده از داده‌های POI تسهیلات شهری گزارش می‌کند. بخش آخر مطالعه را به پایان می رساند.

2. بررسی ادبیات

در اصل، روش‌های فضایی مسطح به طور مستقیم برای اندازه‌گیری تغییرات فضایی رویدادهای شبکه [ 12 ، 21 ] و همبستگی خودکار تصادفات ترافیکی شبکه برای اولین بار با استفاده از آمار فضایی جهانی مورد بررسی قرار گرفت [ 22 ]. در سال‌های اخیر، نگرانی اصلی تحلیل فضایی، کشف غیرایستایی فرآیندهای فضایی و شناسایی غلظت‌های خاص با استفاده از آمار فضایی محلی بوده است. در [ 12 ]، شاخص های محلی تداعی فضایی (LISA) [ 23 ] برای شناسایی مناطق داغ ترافیک اعمال شد. با این حال، استفاده از روش‌های مسطح برای پدیده‌های محدود به شبکه می‌تواند منجر به سوگیری سیستماتیک و استنتاج الگوی نامناسب شود [ 21]]. بنابراین، بسیاری از محققین با گسترش روش های مسطح به روش های مبتنی بر شبکه، پیشرفت چشمگیری داشته اند. به عنوان مثال، دو روش متداول مبتنی بر رویداد، تخمین چگالی هسته مسطح (KDE) و روش‌های تابع K مسطح به شبکه KDE [ 4 ، 6 ، 14 ، 15 ] و تابع K شبکه [ 4 ، 5 ، گسترش یافته است . 11 ، 24 ] روش ها، به ترتیب. با استفاده از رویکرد پیوند-ویژگی، یک روش اکتشافی به نام شاخص‌های محلی خوشه‌های محدود به شبکه (LINCS) برای تشخیص خوشه‌بندی مقیاس محلی رویدادهای شبکه معرفی شد [ 16] .]. دو نوع روش LINCS، یعنی ILINCS و GLINCS، به ترتیب گسترش شبکه آمار محلی Moran’s I و محلی Getis-Ord G هستند.

با توجه به مدیریت تغییرات پس‌زمینه در توزیع پایه، یک رویکرد رادیکال بازسازی فرآیند فضایی خود وقوع رویداد تحت فرضیه صفر عدم وجود الگوی فضایی است [ 4 ]. دو فرض جایگزین وجود دارد که می تواند در این شبیه سازی استفاده شود [ 16 ]. در رویکرد اول، احتمال یک رویداد بودن هر واحد فضایی در توزیع پایه در شبکه ثابت است و تعداد رویدادهای مشاهده‌شده برای هر پیوند از توزیع پواسون پیروی می‌کند [19 ]]. رویکرد دوم فرض می‌کند که احتمال وقوع یک رویداد برای یک پیوند متناسب با مقدار پایه پیوند است، که می‌تواند با استفاده از توزیع تهی مبتنی بر دو جمله‌ای، مانند توزیع دوجمله‌ای، توزیع چند جمله‌ای یا توزیع دوجمله‌ای منفی شبیه‌سازی شود [ 25 ] .

همانطور که قبلاً بحث شد، تنوع تصادفی که از تخمین نمونه کوچک حاصل می شود باید در تحلیل فضایی مبتنی بر شبکه در نظر گرفته شود. یکی از امتیازات قابل توجه رویکرد بیزی توانایی آن برای ایجاد تخمین های قوی در حضور داده های پراکنده یا رویدادهای نادر است [ 25 ]، که برای اولین بار در منطقه نقشه برداری بیماری [ 26 ] اعمال شد. اصل اساسی روش های بیزی این است که داده های نامطمئن را می توان با ترکیب آنها با اطلاعات قبلی تقویت کرد [ 25]]، که استنتاج بیزی را به یک روش برآورد جذاب در بسیاری از زمینه ها تبدیل می کند. در نقشه برداری بیماری، از آمار بیزی برای حذف بخشی از مولفه تصادفی از نقشه استفاده شده است تا با در نظر گرفتن روابط همسایگی در داده ها، تخمین های همواری از خطر نسبی در هر منطقه تولید شود [19 ، 27 ] . روش‌های مبتنی بر آمار بیزی نیز در زمینه‌های دیگری که از تجزیه و تحلیل فضایی با ناحیه کوچک استفاده می‌کنند، مانند جرم [ 28 ]، آلودگی هوا [ 29 ] و تصادفات ترافیکی [ 30 ] اجرا شده‌اند. با این حال، کاربرد رویکردهای بیزی برای کشف تنوع فضایی پدیده‌های محدود به شبکه هنوز از نظر تعداد مطالعات موجود محدود است.

تشخیص داده شده است که تخمین بیزی نشان دهنده یک مبادله بین دقت بهبود یافته و معرفی سوگیری است [ 31 ]. در مورد نقشه‌برداری تجربی بیماری بیزی، تخمین‌های پسین خطر بیماری از نظر فضایی متغیر بر اساس ترکیب وزنی از دو مؤلفه، یعنی خطر محلی و اطلاعات قبلی از مناطق اطراف ارزیابی می‌شوند [25، 27 ] .]. رابطه بین دو مؤلفه به اندازه جمعیت در منطقه محلی بستگی دارد. ریسک هموارسازی شده که می‌توان با استفاده از پیشین بر اساس میانگین جهانی همسایگان تخمین زد، پایدارتر است و عدم اطمینان کمتری دارد. علاوه بر این، پیشین را می توان به عنوان یک ساختار سلسله مراتبی یا چند سطحی مرتب کرد که می تواند تخمین توزیع پارامترها مانند پیچیدگی قبلی را ساده کند. با این حال، از آنجایی که روش‌های بیزی تجربی به سمت داده‌های خلاصه شده از مناطق همسایه تمایل دارند، دو نوع روش بیزی برای رفع محدودیت‌های تخمین‌های تجربی، یعنی مدل‌های بیزی سلسله مراتبی [ 26 ] و مدل BYM معرفی شده توسط Besag، York، توسعه داده شده است. و مولیه [ 32 ].

استفاده از مدل‌های سلسله مراتبی برآورد شده در چارچوب بیزی برای محاسبه سطوح مختلف تغییرپذیری داده‌های مکانی در سال‌های اخیر به خوبی تثبیت شده است. مدل‌های بیزی سلسله مراتبی در ابتدا در زمینه تجزیه و تحلیل تصویر توسعه یافتند و متعاقباً به طور گسترده در نقشه‌برداری بیماری و مطالعات اکولوژیکی مورد استفاده قرار گرفتند. در آمارهای فضایی مرسوم، نتایج یک مدل رگرسیون تنها مقدار کمی از واریانس را توضیح می‌دهد [ 2 ، 25 ]. با این حال، در مدل‌های بیزی سلسله مراتبی، «واریانس اضافی» غیرقابل توضیح [ 25 ، 26 ] توسط اثرات همبسته فضایی یا اثرات ناهمگنی فضایی [ 27 ، 31 ، 33 ] نشان داده می‌شود.]. برخلاف دیگر مدل‌های بیزی، وابستگی فضایی در مدل‌های بیزی سلسله مراتبی در نظر گرفته می‌شود. تخمین پارامترها برای یک واحد فضایی معین با قدرت “قرض گرفتن” از واحدهای فضایی همسایه به دست می آید [ 19 ، 31 ]. علاوه بر این، عبارت «سلسله مراتبی» نشان می‌دهد که نتایج مشاهده‌شده به‌طور مشروط بر روی مجموعه‌ای از پارامترها مدل‌سازی می‌شوند که به خود یک مقدار احتمالی بر حسب پارامترهای دیگر داده می‌شوند، که در آمار بیزی به عنوان فراپارامترها تعریف می‌شوند. در استنباط بیزی، تخمین های پسین را می توان از ترکیب وزنی تخمین های محلی (که احتمال نیز نامیده می شود) و تخمین ها در واحدهای فضایی اطراف تولید کرد. تخمین های بیزی تجربی نادقیق هستند و تمایل دارند به سمت میانگین جهانی بیش از حد هموار شوند [ 31]، در حالی که در روش های بیزی کامل، هایپرپارامترها دارای توزیع های فوق پیشین هستند. در نتیجه، برآوردها برای هر واحد فضایی بهتر به مقدار واقعی تقریب می‌یابند [ 32 ].

این مطالعه تلاش می‌کند تا یک روش بیزی برای تجزیه و تحلیل تغییرات فضایی در پدیده‌های محدود شبکه ایجاد کند. عدم قطعیت بالا و تغییرات تصادفی داده‌های مبتنی بر ویژگی پیوند با اعمال یک مدل بیزی سلسله مراتبی در فضای شبکه حذف می‌شوند. برای بررسی عملکرد روش بیزی پیشنهاد شده در اینجا، یک شبکه فرضی مبتنی بر مطالعه شبیه‌سازی و یک مطالعه موردی به ترتیب با داده‌های POI تسهیلات شهری در شنژن، چین انجام می‌شود. علاوه بر این، ما دو نوع روش LINCS را برای شناسایی خوشه‌های مقیاس محلی اعمال می‌کنیم.

3. مواد و روشها

3.1. مدل های بیزی سلسله مراتبی برای داده های محدود شده در شبکه

در این مطالعه، ما بر روی شبکه‌های ملموس مانند شبکه‌های جاده‌ای و شبکه‌های رودخانه‌ای تمرکز می‌کنیم. پیوندها در شبکه به عنوان لبه های بین دو تقاطع تعریف می شوند و می توانند به BSU تقسیم شوند. اجازه دهید شبکه ای را در نظر بگیریم که از

n

BSUs، و اجازه دهید

y_{i}

یک مقدار شمارش بهره مشاهده شده در BSU باشد

i (i = 1, \dots, I)

. همانطور که در بالا ذکر شد، اثرات توزیع پایه باید در هنگام اندازه گیری تغییرات فضایی پدیده های محدود شده در شبکه در نظر گرفته شود. در این مطالعه، ما یک مدل پواسون را برای شمارش ها در نظر می گیریم و مدل های فضایی بیزی را در چارچوب پواسون با یک پیوند لجستیک فرموله می کنیم. بسط این مدل به حالت دو جمله ای ساده است. در چارچوب سلسله مراتبی بیزی که در نظر می گیریم، احتمال پواسون شمارش های مشاهده شده اولین سطح مدل است که برای مدل سازی تغییرپذیری درون بخش شمارش رویداد مشروط به پارامترهای ریسک ناشناخته استفاده می شود. توزیع های قبلی این پارامترها در سطح دوم مدل مشخص می شود که در آن وابستگی فضایی نیز اندازه گیری می شود.

در سطح اول، مدل احتمال فرض می‌کند که رویداد مشاهده شده مهم است

y_{i}

برای هر BSU توزیع پواسون را دنبال کنید

π_{i}

برای گرفتن تنوع درون بخش شمارش:

y من ~ پ یا من هستم (___π من)

(1)

از این رو،

π_{i}

تخمینی از تعداد واقعی رویدادها در BSU است

i

، که می تواند به صورت زیر محاسبه شود:

π من = E من \times آر من

(2)

جایی که $R_{i}$ نسبت بین تعداد رویدادهای مشاهده شده است $y_{i}$ و رویداد مورد انتظار مهم است $E_{i}$ برای BSU $i$ ، که می توان آن را ریسک نسبی نامید. $E_{i}$ از رابطه زیر بدست می آید:

E من = \sum من j = 1 y j \sum من j = 1 n j \times n من, i = 1, \dots, I

(3)

آر من = y من E من آر من = y من E من

(4)

جایی که $n_{i}$ تعداد کل رویدادها برای BSU است $i$ . شناسایی یک توزیع پایه معقول که تا حد زیادی به پدیده های مورد علاقه بستگی دارد، مهم است. به عنوان مثال، هنگامی که امکانات خرید یا تصادفات ترافیکی موضوعات تحقیق هستند، تعداد انواع POI یا حجم ترافیک را می توان به عنوان توزیع پایه مربوطه مشاهده کرد. در یک زمینه رگرسیون بیزی، ریسک نسبی در BSU $i$ را می توان به عنوان تابعی از یک سری متغیرهای توضیحی [ 31 ] پارامتر کرد. در سطح دوم مدل، نسبت را تقسیم کردیم $R_{i}$ در مقیاس لگاریتمی به یک برش کلی $α$ و جلوه های فضایی اصلی $S_{i}$ ، که فرض می شود تقریباً به طور معمول توزیع شده است:

ورود به سیستم (آر من) = α + اس من

(5)

بنابراین، تخمین تعداد واقعی رویدادها برای BSU

i

از رابطه زیر بدست می آید

ورود به سیستم (π من) = ورود به سیستم (E من) + α + اس من

(6)

یک توزیع قبلی غیر اطلاعاتی (توزیع مسطح) برای عبارت رهگیری داده شده است

α

. وابستگی فضایی با استفاده از یک ماتریس وزن های فضایی نشان داده می شود که مجموعه ای از همسایگان فضایی را تعریف می کند.

δ_{i}

برای هر واحد

i

. ماتریس وزن W

= (w_{i j})

سپس برای اندازه گیری مجاورت بین بخش ها در شبکه داده شده تعریف می شود. در ساده ترین حالت،

w_{i j} = 1

اگر بخش

i

j

به اشتراک گذاشتن یک گره مشترک، و در غیر این صورت 0 است، که در این مقاله با نشان داده شده است

i ~ j

; همچنین ممکن است با فاصله شبکه بین نقاط میانی بخش ها تعریف شود. اگرچه ماتریس وزن در فضای شبکه در برخی شرایط می تواند پیچیده باشد، ما دو نوع همسایگی فضایی فوق را به دلیل کاربردهای بسیار گسترده تری در این زمینه در نظر می گیریم. وابستگی فضایی با استفاده از یک فرآیند اتورگرسیو شرطی (CAR) مدل‌سازی می‌شود [ 19 ]. با توجه به ماتریس W ، توزیع شرطی مجموعه ای از پارامترها

μ_{i}

مشخص شده است توسط:

p (μ من ∣ ∣ μ j, j \neq i) ~ N (μ من ¯ ¯ ¯ ، σ 2 ε / ک من)

(7)

μ من ¯ ¯ ¯ = 1 ک من \sum من ~ ج μ j

(8)

جایی که $σ_{ε}^{2}$ یک پارامتر واریانس ناشناخته است، $k_{i}$ تعداد همسایگان قطعه است $i$ ، $μ = (μ_{1}, .., μ_{I})$ نشان دهنده اثرات تصادفی در مدل های فضایی بیزی است، و $\bar{μ_{i}}$ انتظار مشروط است $μ_{i}$ . بنابراین، مقدار یک پارامتر مرتبط با بخش $i$ تحت تأثیر میانگین ارزش همسایگان خود با تنوع اضافی قرار می گیرد. پارامتر واریانس $σ_{ε}^{2}$ میزان تغییرات بین اثرات تصادفی را کنترل می کند. این ساختار واریانس این واقعیت را تشخیص می دهد که در حضور همبستگی فضایی قوی، هر چه یک واحد همسایه های بیشتری داشته باشد، اطلاعات بیشتری در مورد مقدار اثر تصادفی آن در داده ها وجود دارد. با این حال، یک وابستگی مکانی قوی توسط فرآیند CAR تعریف می‌شود که تنها یک پارامتر آزاد دارد که به واریانس شرطی مرتبط است. $σ_{ε}^{2}$ . اثر فضایی اصلی را می توان به دو بخش تقسیم کرد: یک اثر بدون ساختار فضایی و یک اثر ساختاری فضایی که به ترتیب نشان دهنده ناهمگونی و وابستگی فضایی است [ 19 ]. بنابراین، برای افزایش انعطاف‌پذیری روش، یک مدل BYM کانولوشن را برای ترکیب فرآیند CAR (اثر ساختاری فضایی) با یک جزء نرمال غیرساخت‌یافته (اثر بدون ساختار فضایی) اعمال می‌کنیم. مدل حاصل را می توان به صورت زیر نوشت:

اس من ~ ن (μ من ، σ 2 ν), i = 1, \dots, I

(9)

μ من ~ سی A R (W, σ 2 ε)

(10)

جایی که $σ_{ν}^{2}$ واریانس جزء بدون ساختار است. ما سطح سوم مدل را بیشتر تعریف می کنیم تا پارامترهای تغییرات که در سطح دوم درگیر هستند (معادلات (9) و (10)) خود به عنوان توزیع های ناشناخته و داده شده بیش از پیش در نظر گرفته شوند. برای انحراف استاندارد سلسله مراتبی، ما یک توزیع یکنواخت را در بازه (0100) مشخص می کنیم زیرا این محدوده به اندازه کافی گسترده است تا هر مقدار واقعی را در مدل سازی تبدیل شده با ورود به سیستم پوشش دهد [19 ] .

استنتاج بیزی مبتنی بر توزیع مشترک همه پارامترها است که در گذشته دشوار و غیرقابل حل تلقی می شد. در این مطالعه میانگین خلفی تمامی پارامترها با استفاده از الگوریتم‌های زنجیره مارکوف مونت کارلو (MCMC) برآورد شد. ما از نرم افزار رایگان WinBUGS که بر اساس الگوریتم های MCMC است، برای پیاده سازی مدل استفاده کردیم [ 34 ]. معیار اطلاعات انحراف (DIC) برای ارزیابی خوب بودن برازش مدل اعمال می شود. اگر اختلاف DIC بیشتر از 5 باشد، مدل با کمترین DIC به عنوان بهترین مدل انتخاب می شود [ 35]]. DIC که یک تعمیم مدلسازی سلسله مراتبی از معیار اطلاعات آکایک (AIC) و معیار اطلاعات بیزی (BIC) است، به ویژه در مسائل انتخاب مدل بیزی که در آن توزیع های خلفی مدل ها بر اساس شبیه سازی MCMC به دست می آید، مفید است [19 ] . .

3.2. رویکردهای ILINCS و GLINCS

بر اساس آمار مسطح Moran’s I، تجزیه و تحلیل خودهمبستگی شبکه، ماتریس وزن فضایی را تغییر می دهد تا اتصال شبکه بین پیوندها را منعکس کند. مانند آماره محلی I، آماره محلی G را می توان برای تحلیل پدیده های محدود شده در شبکه با اصلاح ماتریس وزن [ 13 ، 15 ] اعمال کرد. هدف آمار محلی I تعیین همبستگی خودکار بین یک منطقه و همسایگان آن است. با این حال، آماره محلی G غلظت ویژگی های یک متغیر را در اطراف یک منطقه اندازه گیری می کند [ 36 ]. در [ 37 ]، نویسندگان آمار G محلی را اصلاح کردند تا متغیر غیرمثبت و ماتریس وزن غیر باینری باشد. دو نسخه از آمار محلی G وجود دارد، یعنی

G_{i} (d)

G_{i}^{*} (d)

. تنها تفاوت بین این دو آمار این است که آیا واحد

i

خود شامل می شود یا خیر. در [ 16 ]، نویسندگان انجام تجزیه و تحلیل با آمار محلی I و G ^* را به طور همزمان توصیه کردند زیرا این دو آمار مکمل یکدیگر هستند.

آمار موران I و Getis-Ord G از توزیع نرمال مجانبی پیروی می کند که فرض نرمال بودن یا فرض تصادفی سازی برقرار باشد [ 16 ، 20 ]. با این حال، در زمینه تشخیص خوشه در مقیاس محلی در فضای شبکه، فرض تصادفی سازی بر فرض نرمال بودن ترجیح داده می شود زیرا هر پیوند معمولاً به تعداد نسبتاً کمی از پیوندهای دیگر متصل است [23 ] . برای اندازه‌گیری توزیع‌های صفر آمار محلی، استنتاج آماری مبتنی بر شبیه‌سازی مونت کارلو در مطالعات قبلی توصیه شد [ 5 ، 13 ، 23]]. در این مطالعه، ما از روش‌های ILINCS و GLINCS برای کشف الگوهای فضایی محلی در یک شبکه استفاده کردیم، که شبیه‌سازی مونت کارلو را برای ارزیابی اهمیت آماری خوشه‌های شناسایی‌شده ترکیب می‌کند.

3.3. طراحی تحلیل و داده POI

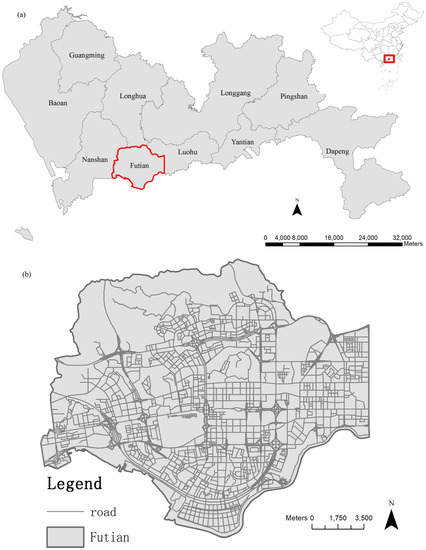
برای نشان دادن اعتبار روش پیشنهادی، دو آزمایش در این مقاله انجام شده است. آزمایش اول شامل یک شبکه فرضی است و آزمایش دوم از داده های شهر شنژن استفاده می کند. در آزمایش اول، این روش برای تجزیه و تحلیل تغییرات تکراری پدیده های پیوند-ویژگی شبیه سازی شده در یک شبکه فرضی ساده شده استفاده می شود. آزمایش دوم از یک سیستم شبکه جاده‌ای و داده‌های POI تأسیسات شهری برای سال 2013 از منطقه Futian، منطقه پیشرفته شهر شنژن استفاده می‌کند ( شکل 1) .). در مقایسه با سایر شهرهای بزرگ چین، شنژن یک شهر مهاجر جوان با رشد اقتصادی سریع به دلیل صنایع پیشرفته و مالی است. با این حال، از آنجایی که این شهر پر رونق با تراکم جمعیتی بالا است، بررسی توزیع امکانات شهری در سراسر شبکه راه‌ها حائز اهمیت است و این نیاز توجه سیاست‌گذاران و محققان را به خود جلب کرده است [38 ] . ما یک نوع POI تسهیلات شهری را انتخاب کردیم که به احتمال زیاد در شبکه‌های جاده‌ای قرار دارند، مانند هتل‌ها، رستوران‌ها، میخانه‌ها، سینماها و گالری‌های هنری، که فعالیت‌های اوقات فراغت متعددی را برای ساکنان شهری پوشش می‌دهند. تعداد این تسهیلات 4212 است و تعداد کل انواع POI در منطقه مورد مطالعه به عنوان توزیع پایه در نظر گرفته می شود.

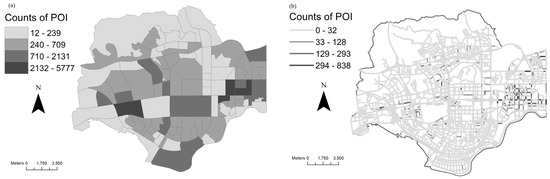
برای اعمال LINCS و روش های پیشنهادی، لازم است POI های مبتنی بر رویداد به داده های مبتنی بر ویژگی پیوند تبدیل شوند. ما روش زیر را در این مطالعه اعمال می کنیم. مسیرها ابتدا با استفاده از یک الگوریتم تقسیم‌بندی شبکه به بخش‌های کوتاه‌تر در نقاط مرجع تقسیم می‌شوند [ 13 ، 16 ]. با در نظر گرفتن 1 کیلومتر به عنوان طول استاندارد BSU، فرآیند تقسیم فوق منجر به 4372 BSU برای 651 کیلومتر شبکه جاده در منطقه مورد مطالعه می شود ( شکل 2) .ب). ثانیاً، تعداد امکانات شهری را در امتداد بخش‌های شبکه می‌شماریم و مقادیر حاصل را به BSUs به عنوان ویژگی‌های جدید اختصاص می‌دهیم. برای جلوگیری از اثرات لبه، تسهیلاتی که در گره های انتهایی بیش از یک BSU قرار دارد، به طور تصادفی به یکی از BSU ها اختصاص داده می شود. در نهایت، در روش های LINCS، تعداد تخصیص یافته POI تسهیلات برای هر BSU با توجه به توزیع پایه استاندارد می شود که با تعداد کل POI در مطالعه موردی تقریب می شود. با استفاده از روش مونت کارلو، آمارهای محلی برای شناسایی الگوی فضایی در شبکه داده شده شبیه‌سازی می‌شوند [ 13 ، 16]]. روش پیشنهادی که مبتنی بر مدل بیزی سلسله مراتبی است، در WinBUGS پیاده سازی شده است. برای هر مدل در مطالعه فرضی، سه زنجیره MCMC موازی که هر کدام شامل 10000 تکرار MCMC هستند با نمودارهای سری زمانی و آمار گلمن-روبین [ 39 ] شبیه‌سازی و تجسم می‌شوند. توزیع های خلفی پارامترهای ناشناخته پس از سوزاندن 1000 تکرار به دست می آیند. ما یک دوره طولانی‌تر را برای مطالعه موردی اعمال می‌کنیم (50000 تکرار پس از 10000 تکرار سوختن)، و تخمین‌های پسین به‌عنوان ورودی برای محاسبه LINCS بدون تعدیل برای توزیع پایه استفاده می‌شوند. شکل 2 تغییرات فضایی توزیع پایه را در منطقه مورد مطالعه توصیف می کند.

4. نتایج و بحث

4.1. یک شبکه فرضی ساده شده

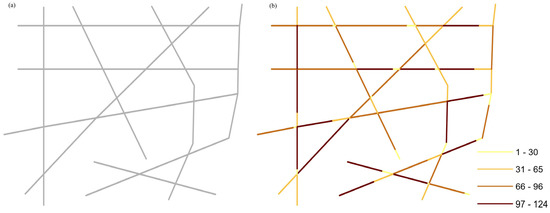
در این بخش، روش پیشنهادی ابتدا با تجزیه و تحلیل یک پدیده محدود شبکه شبیه‌سازی‌شده که توسط ویژگی‌های پیوند در یک شبکه فرضی ساده‌شده نشان داده شده است، آزمایش می‌شود. طول شبکه جاده ساده شده 10 کیلومتر است. با استفاده از طول استاندارد BSU 200 متری، شبکه ساده شده به 80 BSU تقسیم می شود. سپس، 5000 رویداد را به صورت تصادفی در شبکه توزیع می کنیم تا توزیع پایه را نشان دهیم. شکل 3 شبکه فرضی ساده شده و توزیع فضایی رویدادهای شبکه شبیه سازی شده را توصیف می کند.

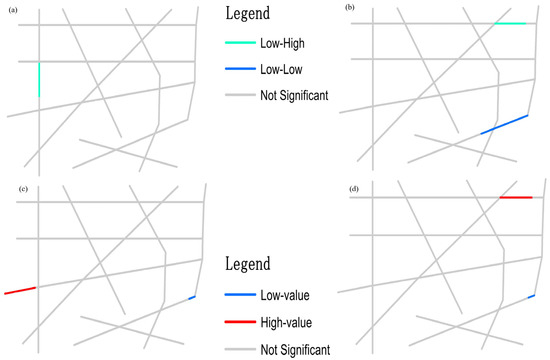
از آنجایی که الگوهای فضایی ممکن است به طول BSU بستگی داشته باشند، ما همچنین یک طول استاندارد کوتاه‌تر BSU، 100 متر، برای اجرای بخش‌بندی شبکه اعمال می‌کنیم. دو نوع ماتریس وزن فضایی، ماتریس مبتنی بر گره و ماتریس مبتنی بر فاصله نیز استفاده می شود. علاوه بر این، ما مجموعه‌ای از رویدادهای نقطه‌ای توزیع‌شده تصادفی را برای نمایش پدیده شبکه مشاهده‌شده شبیه‌سازی می‌کنیم و توزیع‌های فضایی رویدادها در مدل‌هایی با طول BSU و تعداد رویداد یکسان هستند. میز 1آمار خلاصه روش پیشنهادی را نشان می دهد. نتایج نشان می‌دهد که مدلی که دارای 50 رویداد شبکه با طول استاندارد BSU 200 است، عملکرد بالاتری با DIC کمتر نشان می‌دهد و تفاوت قابل‌توجهی در خواص هموارسازی مدل CAR با استفاده از دو نوع ماتریس وزن فضایی وجود ندارد. زیرا تفاوت در DIC کمتر از 5 است. شکل 4 a تخمین خام ریسک نسبی را نشان می دهد. بر اساس نتایج M2 _، توزیع فضایی برآوردهای پسین در شکل 4 ب نشان داده شده است. مقایسه شکل 4a،b نشان می دهد که مقادیر شدید ریسک خام را می توان با روش پیشنهادی، که بر اساس آمار بیزی، برای پدیده های محدود شده در شبکه است، هموار کرد. این می تواند به این معنا باشد که تغییرات فضایی تخمین ریسک در یک فضای شبکه به وابستگی فضایی و تنوع اضافی نسبت به فضای مسطح نسبت داده می شود. سپس روش‌های LINCS برای شناسایی خوشه‌های فضایی در پدیده شبیه‌سازی شده بر اساس نتایج M2 اعمال می‌شوند ₍ شکل 5 ).

شکل 5 a,c نتایج حاصل از روش های LINCS تنظیم شده برای توزیع پایه را با 999 جایگشت شرطی و سطح معنی داری 0.01 نشان می دهد. یک BSU به عنوان دارای همبستگی منفی معنادار ( شکل 5 الف) شناسایی شده است و غلظت های فضایی قابل توجهی در پدیده شبیه سازی شده وجود دارد ( شکل 5 ج). با استفاده از تخمین های پسین به عنوان مقادیر ویژگی BSU ها برای محاسبه LINCS و با استفاده از سطح معنی داری 0.01، دو BSU دارای همبستگی خودکار شبکه قابل توجهی هستند ( شکل 5 ب)، و شکل 5 d توزیع غلظت های قابل توجه مقادیر را نشان می دهد. . مقایسه شکل 5a،b نشان می دهد که تفاوت های قابل توجهی در نتایج بین ILINCS و روش پیشنهادی وجود دارد. پیوندهای با غلظت قابل توجه مقادیر شناسایی شده توسط GLINCS ( شکل 5 ج) همیشه با پیوندهایی با غلظت قابل توجه شناسایی شده توسط روش پیشنهادی مطابقت ندارند ( شکل 5 د). این نشان می‌دهد که وابستگی فضایی می‌تواند عامل اصلی تأثیرگذار بر استنتاج الگوی فضایی باشد و روش‌های شبیه‌سازی، مانند روش‌های MCMC و جایگشت، باید در این زمینه اعمال شود.

4.2. الگوهای فضایی تأسیسات شهری در فوتیان

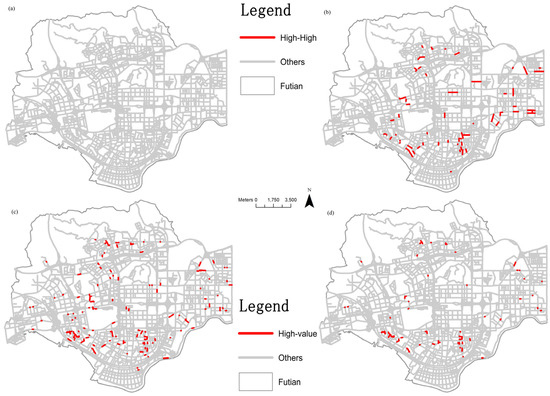
در این بخش، روش پیشنهادی برای تجزیه و تحلیل تغییرات فضایی POI تسهیلات شهری برای فعالیت‌های اوقات فراغت در یک شبکه جاده‌ای پیچیده استفاده می‌شود. در تحقیقات عملی که به موضوعاتی مانند تجزیه و تحلیل فضایی جرایم و تصادفات رانندگی می پردازند، شناسایی الگوهای خودهمبستگی بالا و تمرکز با ارزش بالا بیش از سایرین توجه را به خود جلب می کند. بنابراین، در مطالعه موردی، روش‌های LINCS برای شناسایی نقاط داغ امکانات شهری برای فعالیت‌های اوقات فراغت توزیع شده در طول 651 کیلومتر شبکه جاده‌ای در Futian، شنژن استفاده می‌شود. ساختار شبکه راه ها پیچیده است. این شامل بزرگراه ها، جاده های اولیه، جاده های فرعی و جاده های فرعی است. روش پیشنهادی بر روی یک کامپیوتر شخصی با Intel® پیاده سازی شده ^استCPU Core™ 2 Duo و 4 گیگابایت رم (Lenovo T430) با سیستم عامل 64 بیتی (Windows 7 Professional). نتایج تجربی به صورت فایل‌های شکل ذخیره شده و در نرم‌افزار ArcGIS 10.0 نمایش داده می‌شوند. LINCS بر اساس 999 تکرار شبیه سازی مونت کارلو با استفاده از سطح معنی داری 0.001 و یک ماتریس اتصال باینری محاسبه می شود. ما دو نوع ماتریس وزن فضایی، ماتریس‌های مبتنی بر گره و مبتنی بر فاصله را برای روش پیشنهادی اعمال می‌کنیم. جدول 2 آمار خلاصه روش پیشنهادی را نشان می دهد. نتایج نشان می دهد که تفاوت معنی داری در عملکرد مدل های CAR با استفاده از دو نوع ماتریس فضایی وجود ندارد. توزیع خلفی پارامترهای مدل های بیزی سلسله مراتبی با استفاده از دو نوع ماتریس فضایی در جدول 3 خلاصه شده است .

شکل 6 a,c توزیع آمار محلی را برای شمارش استاندارد POI تنظیم شده برای توزیع پایه نشان می دهد. برای روش پیشنهادی، توزیع خلفی بر اساس سه زنجیره MCMC موازی به دست می‌آید که هر کدام شامل 50000 تکرار پس از 10000 سوختن است. سپس، تخمین های پسین بر اساس مدل CAR مبتنی بر گره به عنوان ورودی برای محاسبه LINCS بدون تنظیم برای توزیع پایه اعمال می شود ( شکل 6 b,d). نتایج تجزیه و تحلیل در مقیاس محلی در جدول 4 خلاصه شده است .

در شکل 6 الف، هیچ همبستگی شبکه با بالا و بالا قابل توجهی در منطقه مورد مطالعه وجود ندارد. در حالی که تعدادی از BSU ها به عنوان دارای الگوهای خوشه بندی قابل توجه و بالا بر اساس ریسک خلفی شناسایی شده اند ( شکل 6 ب). این نشان می‌دهد که روش پیشنهادی مبتنی بر مدل‌های بیزی سلسله مراتبی برای تشخیص نقاط داغ در پدیده‌های محدود شده شبکه مفید است. شکل 6 d نتایج آمارهای محلی را با استفاده از ریسک پسین و بدون تعدیل برای توزیع پایه ارائه می‌کند، که در آن تعداد کمتری از پیوندها به عنوان دارای غلظت‌های با ارزش بالا نسبت به نتایج GLINCS (شکل 6 ج) شناسایی می‌شوند . مقایسه شکل 6c،d نشان می‌دهد که BSUs با غلظت‌های با ارزش بالا با استفاده از ریسک خلفی بدون تعدیل برای توزیع پایه، همیشه خوشه‌های قابل‌توجهی با ارزش بالا را با استفاده از GLINCS نشان می‌دهند. این نشان می دهد که POI های انتخاب شده تمایل به تشکیل یک الگوی خوشه ای با تعدیل برای توزیع پایه دارند و می توان از ریسک پسین برای شناسایی خوشه های امکانات شهری استفاده کرد.

در یک فضای شبکه، وابستگی فضایی هنوز تاثیر قابل توجهی بر تشخیص الگوی فضایی دارد. روش مبتنی بر مدل‌های بیزی سلسله مراتبی می‌تواند بخشی از تغییرپذیری تصادفی ناشی از تخمین نمونه کوچک را حذف کند، که برای کاوش الگوهای فضایی در پدیده‌های محدود شبکه ارزشمند است. علاوه بر این، ترکیب متغیرهای توضیحی در روش پیشنهادی راحت است که می‌تواند برای درک بهتر عوامل تعیین‌کننده فرآیند فضایی آشکار نشده استفاده شود. یک محدودیت قابل توجه این است که ماتریس وزن Wبه عنوان ماتریس وزن فضایی ساده در مطالعه موردی تنظیم شد. اتصالات جاده ای به BSU های 1 کیلومتری تقسیم شدند. اگرچه نتایج این یافته‌ها را تأیید می‌کند که تفاوت قابل‌توجهی در خواص هموارسازی مدل CAR با استفاده از دو نوع ماتریس وزن فضایی وجود ندارد، اغلب ارزشمند است که با بررسی مقادیر متعدد طول استاندارد BSU با مؤثرترین مقیاس خوشه‌بندی جستجو شود. ماتریس های وزنی متعدد در سطح منطقه، ما چندین محله فضایی (به عنوان مثال، ماتریس‌های مبتنی بر مجاورت، مبتنی بر فاصله، و مبتنی بر شباهت) ایجاد کردیم و آنها را در مجموعه داده‌ای بزرگ از پذیرش فشار خون بالا در شنژن اعمال کردیم. نتایج نشان داد که ماتریس‌های وزن فضایی تأثیر محدودی بر عملکرد مدل‌های CAR دارند. اگرچه تعریف همسایگان شبکه یک کار پیچیده است،

5. نتیجه گیری ها

با توجه به پیشرفت مداوم در جمع‌آوری داده‌ها و استنتاج آماری، علایق پژوهشی در تحلیل فضایی از مقیاس میانی به مقیاس خرد برای اندازه‌گیری الگوهای فضایی فرآیندهای فضایی پیچیده تغییر کرده است [23 ]]. به عنوان مثال، در تجزیه و تحلیل تصادف جاده ای، نقطه سیاه تصادف ترافیکی به عنوان یک بخش جاده جداگانه با تعداد زیادی تصادف تعریف می شود. مجموعه ای از بخش های جاده پیوسته با تعداد تصادفات بالا، منطقه داغ تصادف ترافیکی را توصیف می کند. در این مطالعه، ما یک روش مبتنی بر مدل‌های بیزی سلسله مراتبی را برای کشف تغییرات فضایی پدیده‌های محدود شبکه که با یک ویژگی پیوند در رابطه با دو آزمایش مبتنی بر یک شبکه فرضی ساده‌شده و یک شبکه جاده پیچیده در شنژن با تسهیلات شهری 4212 نشان‌داده شده‌اند، اعمال کردیم. POI برای فعالیت های اوقات فراغت. برآوردهای دقیق آماری با ترکیب اطلاعات قبلی از پیوندهای مجاور برای حذف تغییرات تصادفی ناشی از تعداد کمی از مشاهدات ایجاد شد.

در مطالعه موردی، روش پیشنهادی برای کشف تغییرات فضایی POIهای تسهیلات شهری برای فعالیت‌های اوقات فراغت در شنژن، چین و روش‌های LINCS بیشتر برای شناسایی خوشه‌های در مقیاس محلی استفاده شد. در شهرهای مدرن، امکانات شهری مانند امکانات خدمات عمومی اجتماعی، موسسات پزشکی و فروشگاه‌های خرده‌فروشی، اجزای مهمی هستند که برای زندگی روزمره ساکنان شهری ضروری هستند. علاوه بر این، عموماً انتظار می رود که امکانات شهری به دلیل ارتباط ذاتی بین انواع مختلف امکانات شهری، خوشه های فضایی را در فضای جغرافیایی تشکیل دهند. برای مثال، تسهیلات مالی، تسهیلات تجاری و مشاوره، و فروشگاه‌های خرده‌فروشی اغلب در مناطق تجاری مرکزی (CBD)، که یک موضوع مهم برای برنامه‌ریزی شهری است، دسته‌بندی می‌شوند [ 40] .]. با این حال، در مطالعه موردی، ما انواع POI تسهیلات شهری (به عنوان مثال، بانک‌ها، فروشگاه‌های خرده‌فروشی و سینما) و همچنین ارتباط بین انواع مختلف POI (به عنوان مثال، مدارس و مناطق مسکونی) را در نظر نگرفتیم. ادغام این ویژگی ها و اطلاعات در مورد تحرک انسان به طور قابل توجهی سودمندی عملی روش پیشنهادی را افزایش می دهد که می تواند در زمینه های برنامه ریزی شهری و تحقیقات ایمنی به کار رود.

منابع

گترل، فاصله و فضا AC : دیدگاه جغرافیایی . دانشگاه آکسفورد: آکسفورد، بریتانیا، 1983. [ Google Scholar ]
Haining، RP تجزیه و تحلیل داده های فضایی: نظریه و عمل . انتشارات دانشگاه کمبریج: کمبریج، انگلستان، 2003. [ Google Scholar ]
ایلیان، جی. پنتینن، ا. استویان، اچ. Stoyan, D. تحلیل آماری و مدلسازی الگوهای نقطه ای فضایی ; جان وایلی و پسران: هوبوکن، نیوجرسی، ایالات متحده آمریکا، 2008. [ Google Scholar ]
اوکابه، ا. اوکونوکی، ک. Shiode, S. SANET: جعبه ابزاری برای تحلیل فضایی در شبکه. Geogr. مقعدی 2006 ، 38 ، 57-66. [ Google Scholar ] [ CrossRef ]
یامادا، آی. تیل، JC نشانگرهای محلی خوشه‌های محدود به شبکه در الگوهای نقطه‌ای مکانی. Geogr. مقعدی 2007 ، 39 ، 268-292. [ Google Scholar ] [ CrossRef ]
اوکابه، ا. ساتوح، تی. Sugihara, K. یک روش تخمین چگالی هسته برای شبکه ها، روش محاسباتی آن و یک ابزار مبتنی بر GIS. بین المللی جی. جئوگر. Inf. علمی 2009 ، 23 ، 7-32. [ Google Scholar ] [ CrossRef ]
سیاه، خود همبستگی شبکه WR در شبکه حمل و نقل و سیستم های جریان. Geogr. مقعدی 1992 ، 24 ، 207-222. [ Google Scholar ] [ CrossRef ]
اوکابه، ا. یومونو، اچ. Kitamura, M. تجزیه و تحلیل آماری توزیع نقاط در یک شبکه. Geogr. مقعدی 1995 ، 27 ، 152-175. [ Google Scholar ] [ CrossRef ]
اوکابه، ا. کیتامورا، M. یک روش محاسباتی برای تجزیه و تحلیل منطقه بازار در یک شبکه. Geogr. مقعدی 1996 ، 28 ، 330-349. [ Google Scholar ] [ CrossRef ]
اوکابه، ا. Okunuki، K. یک روش محاسباتی برای تخمین تقاضای فروشگاه های خرده فروشی در یک شبکه خیابانی و پیاده سازی آن در GIS. ترانس. GIS 2001 ، 5 ، 209-220. [ Google Scholar ] [ CrossRef ]
یامادا، آی. تیل، JC مقایسه توابع K مسطح و شبکه در تحلیل تصادفات ترافیکی. J. Transp. Geogr. 2004 ، 12 ، 149-158. [ Google Scholar ] [ CrossRef ]
فلاهوت، بی. موچارت، ام. مارتین، ES; توماس، I. خود همبستگی فضایی محلی و روش هسته برای شناسایی مناطق سیاه: یک رویکرد مقایسه ای. اسید. مقعدی قبلی 2003 ، 35 ، 991-1004. [ Google Scholar ] [ CrossRef ]
لو، BPY; Yao, S. شناسایی مناطق داغ تصادف ترافیکی تحت رویکردهای پیوند-ویژگی و مبتنی بر رویداد در یک محیط محدود شبکه. محاسبه کنید. محیط زیست سیستم شهری 2013 ، 41 ، 249-261. [ Google Scholar ] [ CrossRef ]
زی، ز. Yan, J. تخمین تراکم هسته حوادث ترافیکی در فضای شبکه. محاسبه کنید. محیط زیست شهری. 2008 ، 32 ، 396-406. [ Google Scholar ] [ CrossRef ]
نی، ک. وانگ، ز. دو، س. رن، اف. تیان، کیو. یک روش یکپارچه محدود به شبکه برای تشخیص خوشه فضایی و مکان خطر تصادف ترافیک: مطالعه موردی از ووهان، چین. پایداری 2015 ، 7 ، 2662-2677. [ Google Scholar ] [ CrossRef ]
یامادا، آی. Thill، JC نشانگرهای محلی خوشه های محدود به شبکه در الگوهای فضایی نشان داده شده توسط یک ویژگی پیوند. ان دانشیار صبح. Geogr. 2010 ، 100 ، 269-285. [ Google Scholar ] [ CrossRef ]
میلر، HJ مشارکت بالقوه تجزیه و تحلیل فضایی به سیستم های اطلاعات جغرافیایی برای حمل و نقل (GIS-T). Geogr. مقعدی 1999 ، 31 ، 373-399. [ Google Scholar ] [ CrossRef ]
میلر، اچ جی; Wentz، EA بازنمایی و تحلیل فضایی در سیستم های اطلاعات جغرافیایی. ان دانشیار صبح. Geogr. 2003 ، 93 ، 574-594. [ Google Scholar ] [ CrossRef ]
وانگ، ز. دو، س. لیانگ، اس. نی، ک. لین، دی. چن، ی. لی، جی. تجزیه و تحلیل تغییرات فضایی بستری شدن در بیمارستان برای بیماری فشار خون بالا در شنژن، چین. بین المللی جی. محیط زیست. Res. بهداشت عمومی 2014 ، 11 ، 713-733. [ Google Scholar ] [ CrossRef ] [ PubMed ]
گلفاند، AE; دیگل، پی. گوتورپ، پی. Fuentes, M. Handbook of Spatial Statistics ; CRC Press: Boca Raton، FL، USA، 2010. [ Google Scholar ]
اوکابه، ا. Sugihara, K. تجزیه و تحلیل فضایی در طول شبکه ها: روش های آماری و محاسباتی . جان وایلی و پسران: هوبوکن، نیوجرسی، ایالات متحده آمریکا، 2012. [ Google Scholar ]
مشکی، WR؛ توماس، I. تصادفات در بزرگراه های بلژیک: تجزیه و تحلیل خود همبستگی شبکه. J. Transp. Geogr. 1998 ، 6 ، 23-31. [ Google Scholar ] [ CrossRef ]
Anselin، L. شاخص های محلی ارتباط فضایی-LISA. Geogr. مقعدی 1995 ، 27 ، 93-115. [ Google Scholar ] [ CrossRef ]
اوکابه، ا. یامادا، I. روش تابع K در یک شبکه و اجرای محاسباتی آن. Geogr. مقعدی 2001 ، 33 ، 271-290. [ Google Scholar ] [ CrossRef ]
Congdon، P. مدلسازی کاربردی بیزی ; جان وایلی و پسران: هوبوکن، نیوجرسی، ایالات متحده آمریکا، 2014. [ Google Scholar ]
لاوسون، نقشه برداری بیماری بیزی AB : مدلسازی سلسله مراتبی در اپیدمیولوژی فضایی . CRC Press: Boca Raton، FL، USA، 2013. [ Google Scholar ]
بانرجی، اس. کارلین، BP; Gelfand، مدلسازی و تحلیل سلسله مراتبی AE برای داده های فضایی . CRC Press: Boca Raton، FL، USA، 2014. [ Google Scholar ]
لی، جی. هاینینگ، آر. ریچاردسون، اس. بهترین، N. تنوع فضا-زمان در خطر سرقت: یک رویکرد مدل‌سازی فضایی-زمانی بیزی. تف کردن آمار 2014 ، 9 ، 180-191. [ Google Scholar ] [ CrossRef ]
پیرانی، م. گالیور، جی. فولر، GW; Blangiardo، M. مدلسازی فضایی بیزی برای ارزیابی مواجهه کوتاه مدت با آلودگی ذرات در مناطق شهری. J. Expo. علمی محیط زیست اپیدمیول. 2014 ، 24 ، 319-327. [ Google Scholar ] [ CrossRef ] [ PubMed ]
مدل‌های فضایی و زیست‌محیطی MacNab، YC Bayesian برای تجزیه و تحلیل تصادفات و آسیب‌های ناحیه کوچک. اسید. مقعدی قبلی 2004 ، 36 ، 1019-1028. [ Google Scholar ] [ CrossRef ] [ PubMed ]
بهترین، ن. ریچاردسون، اس. تامسون، A. مقایسه مدل های فضایی بیزی برای نقشه برداری بیماری. آمار روش ها Med. Res. 2005 ، 14 ، 35-59. [ Google Scholar ] [ CrossRef ] [ PubMed ]
بساج، ج. یورک، جی. Mollié، A. بازیابی تصویر بیزی، با دو کاربرد در آمار فضایی. ان Inst. آمار ریاضی. 1991 ، 43 ، 1-20. [ Google Scholar ] [ CrossRef ]
برناردینلی، ال. کلیتون، دی. تخمین های مونتومولی، سی بیزی از نقشه های بیماری: اولویت ها چقدر مهم هستند؟ آمار پزشکی 1995 ، 14 ، 2411-2431. [ Google Scholar ] [ CrossRef ] [ PubMed ]
لون، دی جی؛ توماس، ا. بهترین، ن. Spiegelhalter، DJ WinBUGS-یک چارچوب مدلسازی بیزی: مفاهیم، ساختار، و توسعه پذیری. آمار محاسبه کنید. 2000 ، 10 ، 325-337. [ Google Scholar ] [ CrossRef ]
Spiegelhalter، دی جی; بهترین، NG; کارلین، BP; معیارهای لیند، AVD بیزی از پیچیدگی و تناسب مدل. JR Stat. Soc. سر. B آمار روش. 2002 ، 64 ، 583-639. [ Google Scholar ] [ CrossRef ]
گتیس، ع. Ord, JK تجزیه و تحلیل ارتباط فضایی با استفاده از آمار فاصله. Geogr. مقعدی 1992 ، 24 ، 189-206. [ Google Scholar ] [ CrossRef ]
Ord، JK; Getis، A. آمار خودهمبستگی فضایی محلی: مسائل توزیع و یک برنامه کاربردی. Geogr. مقعدی 1995 ، 27 ، 286-306. [ Google Scholar ] [ CrossRef ]
Myint، SW اکتشاف پراکندگی فضایی، الگو، و ارتباط واحدهای عملکردی اجتماعی-اقتصادی در یک سیستم شهری. Appl. Geogr. 2008 ، 28 ، 168-188. [ Google Scholar ] [ CrossRef ]
گلمن، ا. استنتاج روبین، DB از شبیه سازی تکراری با استفاده از توالی های متعدد. آمار علمی 1992 ، 7 ، 457-472. [ Google Scholar ] [ CrossRef ]
او، بی. زو، ایکس. بله، X. گوو، دبلیو. سو، ک. لی، جی. نمودارهای شبکه ورونوی وزن دار برای تحلیل فضایی محلی. محاسبه کنید. محیط زیست سیستم شهری 2015 ، 52 ، 70-80. [ Google Scholar ] [ CrossRef ]

شکل 1. شهر شنژن و منطقه مورد مطالعه: ( الف ) موقعیت منطقه مورد مطالعه (جعبه قرمز). ( ب ) شبکه راه در منطقه مورد مطالعه.

شکل 2. توزیع پایه در منطقه مورد مطالعه: ( الف ) تعداد نقاط مورد علاقه تسهیلات (POI) در 98 جامعه. ( ب ) تعداد POI برای 4372 واحد فضایی اساسی (BSUs).

شکل 3. توزیع فضایی شبکه فرضی و رویدادهای شبکه شبیه سازی شده: ( الف ) یک شبکه فرضی 10 کیلومتری. ( ب ) تعداد 5000 رویداد شبکه به طور تصادفی در 80 BSU توزیع شده است.

شکل 4. توزیع ریسک نسبی: ( الف ) ریسک خام. ( ب ) هموارسازی ریسک.

شکل 5. توزیع خوشه های فضایی، با استفاده از: ( الف ) ILINCS تنظیم شده برای توزیع پایه. ( ب ) ILINCS با استفاده از ریسک پسین و برای توزیع پایه تنظیم نشده است. ( ج ) GLINCS برای توزیع پایه تنظیم شده است. ( د ) GLINCS با استفاده از خطر خلفی و برای توزیع پایه تنظیم نشده است.

شکل 6. نتایج آمار محلی: ( الف ) ILINCS برای توزیع پایه تنظیم شده است. ( ب ) ILINCS با استفاده از ریسک پسین و بدون تعدیل برای توزیع پایه. ( ج ) GLINCS برای توزیع پایه تنظیم شده است. ( د ) GLINCS با استفاده از خطر خلفی بدون تعدیل برای توزیع پایه.

جدول 1. نتایج روش پیشنهادی تحت سناریوهای مختلف.

جدول 2. نتایج روش پیشنهادی با استفاده از دو نوع ماتریس فضایی.

جدول 3. نتایج توزیع خلفی پارامترها.

جدول 4. تعداد BSU با خود همبستگی قابل توجه و بالا (محلی

I_{i}

) و غلظت با ارزش بالا (محلی

G_{i}^{*}

) (سطح معنی داری 001/0).

© 2017 توسط نویسندگان. دارنده مجوز MDPI، بازل، سوئیس. این مقاله یک مقاله با دسترسی آزاد است که تحت شرایط و ضوابط مجوز Creative Commons Attribution (CC BY) ( http://creativecommons.org/licenses/by/4.0/ ) توزیع شده است.

;کاربردهای GIS مقالات

درخواست مشاوره

09120049370

8 صبح تا 12 شب